题目内容
已知关于 的函数
的函数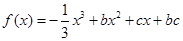 ,其导函数为
,其导函数为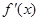 .记函数
.记函数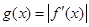 在区间
在区间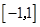 上的最大值为
上的最大值为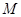 .
.
(1) 如果函数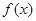 在
在 处有极值
处有极值 ,试确定
,试确定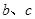 的值;
的值;
(2) 若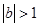 ,证明对任意的
,证明对任意的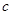 ,都有
,都有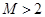 ;
;
(3) 若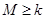 对任意的
对任意的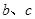 恒成立,试求
恒成立,试求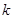 的最大值.
的最大值.
(1)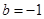 ,
,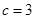 ;(2)证明详见解析;(3)
;(2)证明详见解析;(3)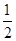 .
.
解析试题分析:本题主要考查导数的运算、利用导数求函数的极值和最值等基础知识,考查学生的转化能力、分析问题解决问题的能力、计算能力.第一问,先对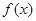 求导,由于
求导,由于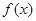 在x=1处有极值
在x=1处有极值 ,则
,则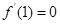 ,
,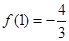 ,列出方程组,解出b和c的值,由于得到了两组值,则需要验证看是否符合已知条件,若不符合需舍掉;第二问,可以利用二次函数图象和性质直接证明
,列出方程组,解出b和c的值,由于得到了两组值,则需要验证看是否符合已知条件,若不符合需舍掉;第二问,可以利用二次函数图象和性质直接证明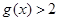 ,也可以利用反证法证明出矛盾,从而得到正确结论;第三问,结合第二问的结论,可以直接得到
,也可以利用反证法证明出矛盾,从而得到正确结论;第三问,结合第二问的结论,可以直接得到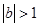 时的情况,当
时的情况,当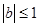 时需分
时需分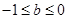 ,
,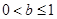 ,
,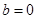 三种情况讨论,最后综合所有情况再得出结论.
三种情况讨论,最后综合所有情况再得出结论.
试题解析:(1) ∵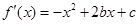 ,由
,由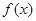 在
在 处有极值
处有极值 ,可得
,可得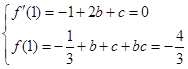 ,解得,
,解得,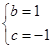 或
或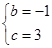 2分
2分
若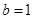 ,
,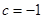 ,则
,则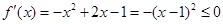 ,此时函数
,此时函数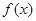 没有极值; 3分
没有极值; 3分
若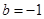 ,
,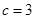 ,则
,则 ,此时当
,此时当 变化时,
变化时,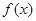 ,
,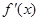 的变化情况如下表:
的变化情况如下表:
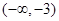
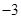
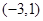
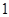
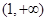
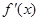
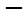

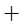

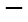
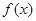
 练习册系列答案
练习册系列答案
家校导学系列答案
新每课一练系列答案

黄冈海淀大考卷单元期末冲刺100分系列答案

课堂新动态系列答案

初中历史与社会思想品德精讲精练系列答案

高效练习系列答案
相关题目
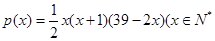 ,且
,且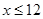 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
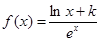 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线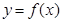 在点
在点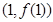 处的切线与x轴平行.
处的切线与x轴平行.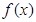 的单调区间;
的单调区间; 其中
其中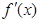 为
为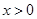 ,
,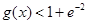 .
.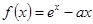 (
(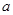 为常数)的图像与
为常数)的图像与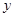 轴交于点
轴交于点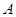 ,曲线
,曲线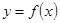 在点
在点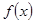 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,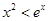 ;
;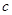 ,总存在
,总存在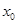 ,使得当
,使得当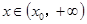 ,恒有
,恒有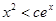 .
.
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数). 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.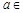 R,函数
R,函数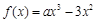 .
.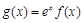 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围. ,
, (
( ).
). 的极值点,求
的极值点,求 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值; 在
在 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中 .
. 与
与 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 ,求
,求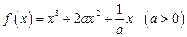 ,则
,则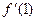 的最小值为
的最小值为