题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的长轴长为6，且椭圆C与圆M：（x﹣2）2+y2= 
的公共弦长为 
．
（1）求椭圆C的方程，
（2）过点P（0，2）作斜率为k（k≠0）的直线l与椭圆C交于两点A，B，试判断在x轴上是否存在点D，使得△ADB为以AB为底边的等腰三角形，若存在，求出点D的横坐标的取值范围，若不存在，请说明理由．
【答案】
（1）
解：由题意可知：2a=6，则a=3，圆M：（x﹣2）2+y2= 
，圆心（2，0），半径为 
，
由题意可知：椭圆经过点（2， ），代入椭圆方程： 
，解得：b2=8，
∴椭圆的标准方程： 
（2）
解：由题意可知直线l：y=kx+2，A（x1，y1），B（x2，y2），
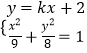，整理得：（9k2+8）x2+36kx﹣36=0，
x1+x2=﹣ 
，x1x2= 
，
假设存在点D（m，0）满足题意，
取AB中点M（x0，y0）则MB⊥AB，
由x0= 
=﹣ 
，则y0=kx0+2= 
，
则M（﹣ ， ），
由题意可知：kkMD=﹣ 
=﹣1，
整理得：9k2m+2k+2m=0，
∴m= 
=﹣ 
≥﹣ 
，
存在点D，且D点横坐标取值范围[﹣ ，+∞）
【解析】（1）由2a=6，则a=3，由圆的方程，可得椭圆过点（2， ），代入椭圆方程，即可求得b的值，求得椭圆方程；（2）设直线l的方程，代入椭圆方程，利用韦达定理及中点坐标公式，求得AB的中点M点坐标，kkMD=﹣1，即可求得m的表达式，利用基本不等式的性质，即可求得点D的横坐标的取值范围．
【题目】某班级数学兴趣小组为了研究人的脚的大小与身高的关系，随机抽测了20位同学，得到如下数据：
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身高x（厘米） | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
脚长y（码） | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身高x（厘米） | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
脚长y（码） | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
（Ⅰ）请根据“序号为5的倍数”的几组数据，求出y关于x的线性回归方程
（Ⅱ）若“身高大于175厘米”为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”为“大码”，“脚长小于等于42码”的为“非大码”．请根据上表数据完成2×2列联表：并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系？
（Ⅲ）若按下面的方法从这20人中抽取1人来核查测量数据的误差：将一个标有1，2，3，4，5，6的正六面体骰子连续投掷两次，记朝上的两个数字的乘积为被抽取人的序号，求：抽到“无效序号（超过20号）”的概率．
附表及公式：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= 
．
【题目】某单位员工
人参加“学雷锋”志愿活动，按年龄分组：第
组
，第
组
,第
组
,第
组
,第
组
，得到的频率分布直方图如图所示.
（1）下表是年龄的频率分布表，求正整数
的值；
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
（2）现在要从年龄较小的第
组中用分层抽样的方法抽取
人，年龄在第组抽取的员工的人数分别是多少？
（3）在（2）的前提下，从这人中随机抽取人参加社区宣传交流活动，求至少有人年龄在第组的概率.
