题目内容
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴,长度单位相同,建立极坐标系,已知圆A的参数方程为 ![]() (其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(Ⅰ)分别写出圆A与圆B的直角坐标方程;
(Ⅱ)判断两圆的位置关系,若两圆相交,求其公共弦长.
【答案】解:(Ⅰ)圆A的参数方程为 ![]() (其中θ为参数),利用平方关系可得圆A:(x﹣1)2+(y+1)2=4.可得圆心A(1,﹣1),半径R=2. 圆B的极坐标方程为ρ=2sinθ,即ρ2=2ρsinθ,利用互化公式可得:圆B:x2+y2﹣2y=0,平方可得:x2+(y﹣1)2=1,可得圆心B(0,1),半径r=1.
(其中θ为参数),利用平方关系可得圆A:(x﹣1)2+(y+1)2=4.可得圆心A(1,﹣1),半径R=2. 圆B的极坐标方程为ρ=2sinθ,即ρ2=2ρsinθ,利用互化公式可得:圆B:x2+y2﹣2y=0,平方可得:x2+(y﹣1)2=1,可得圆心B(0,1),半径r=1.
(Ⅱ)∵|AB|= ![]() =
= ![]() ,而R﹣r=1,R+r=3,
,而R﹣r=1,R+r=3,![]() <3,∴两圆相交,
<3,∴两圆相交,
两个圆的方程相减可得:x﹣2y+1=0.
∴其公共弦长=2 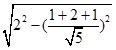 =
= ![]()
【解析】(Ⅰ)圆A的参数方程为 ![]() (其中θ为参数),利用平方关系可得圆A的普通方程.圆B的极坐标方程为ρ=2sinθ,即ρ2=2ρsinθ,利用互化公式可得直角坐标方程.(Ⅱ)利用两圆的圆心距离与半径的和差半径即可判断出两圆相交.两个圆的方程相减可得公共弦所在直线方程,利用弦长公式即可得出.
(其中θ为参数),利用平方关系可得圆A的普通方程.圆B的极坐标方程为ρ=2sinθ,即ρ2=2ρsinθ,利用互化公式可得直角坐标方程.(Ⅱ)利用两圆的圆心距离与半径的和差半径即可判断出两圆相交.两个圆的方程相减可得公共弦所在直线方程,利用弦长公式即可得出.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2016年备受瞩目的二十国集团领导人第十一次峰会于9月4~5日在杭州举办,杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人,为测试培训效果,采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人,对其做G20峰会主题及相关服务职责进行测试,将其所得分数(分数都在60~100之间)制成频率分布直方图如下图所示,若得分在90分及其以上(含90分)者,则称其为“G20通”. 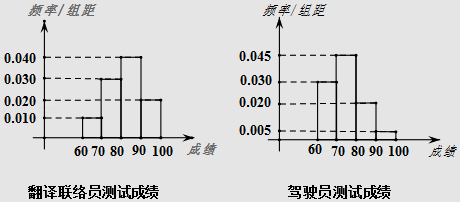
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附参考公式与数据: ![]() .
.
