Question

(本小题满分14分)

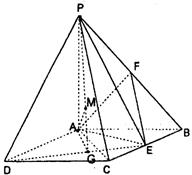
如图：四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.

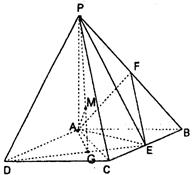
（Ⅰ）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

（Ⅱ）证明：无论点E在BC边的何处，都有PE⊥AF;

（Ⅲ）当BE等于何值时，PA与平面PDE所成角的大小为45°                  

 

Answer 1

【答案】

（I）当点E为BC的中点时，

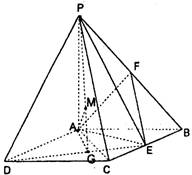
EF与平面PAC平行.

∵在△PBC中，

E、F分别为BC、PB的中点，

∴EF//PC 又EF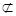平面PAC，

而PC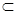平面PAC ∴EF//平面PAC.…4分

（II）证明：见解析；

（Ⅲ）BE=x=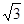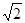－，或BE=x=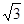+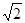（舍）.

【解析】(I)当E为BC的中点时，EF//PC,进而可得EF//平面ABCD.

(II) 无论点E在BC边的何处，都有PE⊥AF,这句话的实质是证明AF⊥平面PBE.

(III) 关键是找出PA与平面PDE所成的角，具体做法：过A作AG⊥DE于G，连PG，又∵DE⊥PA，则DE⊥平面PAG，于是，平面PAG⊥平面PDE，它们的交线是PG，过A作AM⊥PG，垂足为M，则AM⊥平面PDE，则∠APG就是PA与平面PDE所成的角.也可利用向量法求解.                                                        

解法1：（I）当点E为BC的中点时，

EF与平面PAC平行.∵在△PBC中，

E、F分别为BC、PB的中点，

∴EF//PC 又EF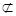平面PAC，

而PC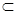平面PAC ∴EF//平面PAC.…4分

   （II）证明：∵PA⊥平面ABCD，BE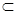平面ABCD，

∴EB⊥PA.又EB⊥AB，AB∩AP=A，AB，AP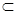平面PAB，

∴EB⊥平面PAB，

又AF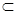平面PAB，∴AF⊥BE. www.7caiedu.cn      

又PA=AB=1，点F是PB的中点，∴AF⊥PB，……………………4分

        又∵PB∩BE=B，PB，BE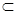平面PBE，∴AF⊥平面PBE.

∵PE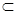平面PBE，∴AF⊥PE.……………………8分

   （Ⅲ）过A作AG⊥DE于G，连PG，又∵DE⊥PA，则DE⊥平面PAG，

于是，平面PAG⊥平面PDE，它们的交线是PG，过A作AM⊥PG，垂足为M，则AM⊥平面PDE，即PA在平面PDE的射影是PM，所以PA与平面PDE所成的角是∠APG=45°.

∴在RtPAG中，PA=AG=1，∴DG=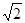，………………10分

设BE=x，∵△AGE≌△ABE，则GE=x，CE=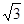－x，

在Rt△DCE中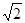，(+x)²=(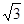－x)²+1²，得BE=x=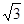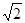－.……12分

解法二： （II）建立图示空间直角坐标系，

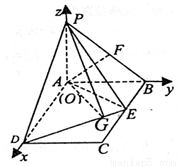
则P（0，0，1），B（0，1，0），

  设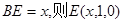

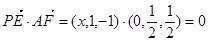∴AF⊥PE …8分

（Ⅲ）设平面PDE的法向量为

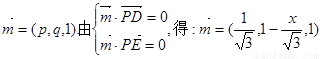
而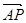=（0，0，1）依题意PA与平面PDE所成角为45°，

所以sin45°=，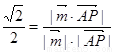

，

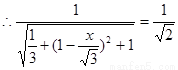得BE=x=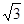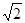－，或BE=x=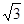+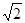（舍）.……………………12分