题目内容
12.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,定点A为双曲线虚轴的一个顶点,过F,A的直线与双曲线的一条渐近线在y轴左侧的交点为B,若$\overrightarrow{FA}$=($\sqrt{2}$-1)$\overrightarrow{AB}$,则此双曲线的离心率是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
分析 设F(c,0),A(0,-b),渐近线方程为y=$\frac{b}{a}$x,求出AF的方程与y=$\frac{b}{a}$x联立可得B($\frac{ac}{a-c}$,$\frac{bc}{a-c}$),利用$\overrightarrow{FA}$=($\sqrt{2}$-1)$\overrightarrow{AB}$,可得a,c的关系,即可求出双曲线的离心率.
解答 解:设F(c,0),A(0,-b),渐近线方程为y=$\frac{b}{a}$x,则
直线AF的方程为$\frac{x}{c}-\frac{y}{b}$=1,与y=$\frac{b}{a}$x联立可得B($\frac{ac}{a-c}$,$\frac{bc}{a-c}$),
∵$\overrightarrow{FA}$=($\sqrt{2}$-1)$\overrightarrow{AB}$,
∴(-c,-b)=($\sqrt{2}$-1)($\frac{ac}{a-c}$,$\frac{bc}{a-c}$+b),
∴-c=($\sqrt{2}$-1)$\frac{ac}{a-c}$,
∴e=$\frac{c}{a}$=$\sqrt{2}$,
故选:A.
点评 本题考查双曲线的性质,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.定义运算:$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,若将函数f(x)=$|\begin{array}{l}{\sqrt{3}}&{sinx}\\{1}&{cosx}\end{array}|$的图象向左平移m(m>0)个单位长度后,所得图象关于y轴对称,则m的最小值是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
17.设集合M={1,4,5},N={0,3,5},则M∩N=( )
| A. | {1,4} | B. | {0,3} | C. | {0,1,3,4,5} | D. | {5} |
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的渐近线与圆x2+(y-2)2=1相交,则该双曲线的离心率的取值范围是( )
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (2.+∞) | D. | (1,2) |
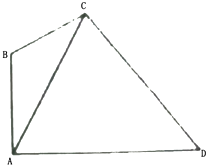 如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=27,设∠ACB=θ,C点到AD的距离为h.
如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=27,设∠ACB=θ,C点到AD的距离为h.