题目内容
20.ABCD是矩形,AB=4,AD=3,沿AC将△ADC折起到△AD′C,使平面AD′C⊥平面△ABC,F是AD′的中点,E是AC上的一点,给出下列结论:①存在点E,使得EF∥平面BCD′;
②存在点E,使得EF⊥平面ABD′;
③存在点E,使得D′E⊥平面ABC;
④存在点E,使得AC⊥平面BD′E.
其中正确结论的序号是①③.(写出所有正确结论的序号)
分析 ①存在AC中点E,则EF∥CD′,利用线面平行的判定定理可得EF∥平面BCD′;
②若EF⊥平面ABD′,则平面ADC⊥平面ABD′,显然不成立;
③D′E⊥AC,利用面面垂直的性质,可得D′E⊥平面ABC;
④因为ABCD是矩形,AB=4,AD=3,所以B,D′在AC上的射影不是同一点,所以不存在点E,使得AC⊥平面BD′E.
解答 解:①存在AC中点E,则EF∥CD′,利用线面平行的判定定理可得EF∥平面BCD′,正确;
②若EF⊥平面ABD′,则平面ADC⊥平面ABD′,显然不成立,故不正确;
③D′E⊥AC,利用面面垂直的性质,可得D′E⊥平面ABC,正确;
④因为ABCD是矩形,AB=4,AD=3,所以B,D′在AC上的射影不是同一点,所以不存在点E,使得AC⊥平面BD′E,故不正确;
故答案为:①③.
点评 本题考查线面平行的判定,考查面面垂直的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
11.设函数f(x)=$\left\{\begin{array}{l}{{3}^{-x},x<1}\\{{x}^{2},x>1}\end{array}\right.$,若f(x)>9,则x的取值范围是( )
| A. | (-∞,-2]∪[3,+∞) | B. | (-2,3) | C. | (-∞,-3)∪(2,+∞) | D. | (-∞,-2)∪(3,+∞) |
5.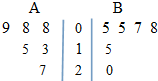 某普通高中共有36个班,每班40名学生,每名学生都有且只有一部手机,为了解该校学生对A,B两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校6个班的学生进行统计,得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:
某普通高中共有36个班,每班40名学生,每名学生都有且只有一部手机,为了解该校学生对A,B两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校6个班的学生进行统计,得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:
(Ⅰ)随机选取1名该校学生,估计该生持有A品牌手机的概率;
(Ⅱ)随机选取1名该校学生,估计该生持有A或B品牌手机且感到满意的概率;
(Ⅲ)A,B两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)
 某普通高中共有36个班,每班40名学生,每名学生都有且只有一部手机,为了解该校学生对A,B两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校6个班的学生进行统计,得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:
某普通高中共有36个班,每班40名学生,每名学生都有且只有一部手机,为了解该校学生对A,B两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校6个班的学生进行统计,得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:满意度 品牌 | 满意 | 不满意 |
| A | 80% | 20% |
| B | 60% | 40% |
(Ⅱ)随机选取1名该校学生,估计该生持有A或B品牌手机且感到满意的概率;
(Ⅲ)A,B两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)
12.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,定点A为双曲线虚轴的一个顶点,过F,A的直线与双曲线的一条渐近线在y轴左侧的交点为B,若$\overrightarrow{FA}$=($\sqrt{2}$-1)$\overrightarrow{AB}$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
10.已知向量$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(sinα,cosα),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则tan2α=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |