题目内容
已知双曲线x2- =1.
=1.

(1)若一椭圆与该双曲线共焦点,且有一交点P(2,3),求椭圆方程.
(2)设(1)中椭圆的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上的一动点,且在x轴上方,直线AN与椭圆交于点M.若AM=MN,求∠AMB的余弦值;
(3)设过A、F、N三点的圆与y轴交于P、Q两点,当线段PQ的中点为(0,9)时,求这个圆的方程.
(1)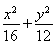 =1(2)-
=1(2)-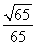 (3)x2+y2+2x-18y-8=0
(3)x2+y2+2x-18y-8=0
【解析】(1)∵双曲线焦点为(±2,0),设椭圆方程为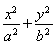 =1(a>b>0).
=1(a>b>0).
则 ∴a2=16,b2=12.故椭圆方程为
∴a2=16,b2=12.故椭圆方程为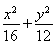 =1.
=1.
(2)由已知,A(-4,0),B(4,0),F(2,0),直线l的方程为x=8.
设N(8,t)(t>0).∵AM=MN,∴M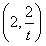 .
.
由点M在椭圆上,得t=6.
故所求的点M的坐标为M(2,3).
所以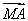 =(-6,-3),
=(-6,-3),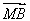 =(2,-3),
=(2,-3),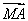 ·
·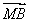 =-12+9=-3.
=-12+9=-3.
cos∠AMB= =
=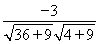 =-
=-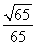 .
.
(3)设圆的方程为x2+y2+Dx+Ey+F=0,将A、F、N三点坐标代入,得
 得
得
圆的方程为x2+y2+2x-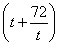 y-8=0,令x=0,得y2-
y-8=0,令x=0,得y2-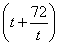 y-8=0.
y-8=0.
设P(0,y1),Q(0,y2),则y1,2= .
.
由线段PQ的中点为(0,9),得y1+y2=18,t+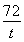 =18,
=18,
此时,所求圆的方程为x2+y2+2x-18y-8=0

练习册系列答案
相关题目










