题目内容
在极坐标系 中,直线
中,直线 的极坐标方程为
的极坐标方程为 是
是 上任意一点,点P在射线OM上,且满足
上任意一点,点P在射线OM上,且满足 ,记点P的轨迹为
,记点P的轨迹为 。
。
(Ⅰ)求曲线 的极坐标方程;
的极坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线 距离的最大值。
距离的最大值。
(Ⅰ)ρ=2sinθ (ρ≠0);(Ⅱ)1+ .
.
解析试题分析:(Ⅰ)借助点P、M的关系求出曲线C2的极坐标方程;(Ⅱ)将极坐标转化成直角坐标下的方程求出圆上的点到直线的最大距离.
试题解析:(Ⅰ)设P(ρ,θ),M(ρ1,θ),依题意有ρ1sinθ=2,ρρ1=4.
消去ρ1,得曲线C2的极坐标方程为ρ=2sinθ (ρ≠0).
(Ⅱ)将C2,C3的极坐标方程化为直角坐标方程,得
C2:x2+(y-1)2=1,C3:x-y=2.
C2是以点(0,1)为圆心,以1为半径的圆,圆心到直线C3的距离d= ,
,
故曲线C2上的点到直线C3距离的最大值为1+ .
.
考点:1、极坐标方程;2、极坐标方程与直角坐标方程的互化.

练习册系列答案
相关题目
 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点. 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .试求曲线
.试求曲线 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 的普通方程;
的普通方程; 为曲线
为曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.  内,直线
内,直线 的参数方程为
的参数方程为
 为参数
为参数 .以
.以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .判断直线
.判断直线 ,
,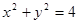 相交与两点A、B,求点P到A、B两点的距离之积。
相交与两点A、B,求点P到A、B两点的距离之积。 =2
=2 .
. (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值. 中以
中以 为极点,
为极点, 轴正半轴为极轴建立坐标系.圆
轴正半轴为极轴建立坐标系.圆 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.


 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数). 轴的交点是
轴的交点是 为曲线
为曲线 的最大值.
的最大值.