题目内容
等比数列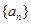 的前
的前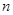 项和为
项和为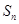 ,已知对任意的
,已知对任意的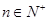 ,点
,点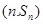 均在函数
均在函数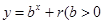 且
且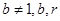 均为常数)的图像上.
均为常数)的图像上.
(Ⅰ)求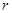 的值;
的值;
(Ⅱ)当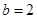 时,记
时,记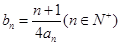 ,求数列
,求数列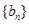 的前
的前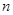 项和
项和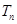 .
.
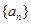 的前
的前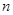 项和为
项和为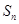 ,已知对任意的
,已知对任意的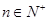 ,点
,点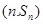 均在函数
均在函数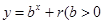 且
且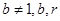 均为常数)的图像上.
均为常数)的图像上.(Ⅰ)求
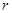 的值;
的值;(Ⅱ)当
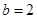 时,记
时,记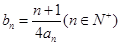 ,求数列
,求数列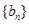 的前
的前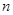 项和
项和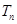 .
.(Ⅰ)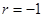 ;(Ⅱ)
;(Ⅱ)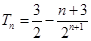 .
.
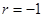 ;(Ⅱ)
;(Ⅱ)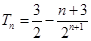 .
.试题分析:(Ⅰ)由已知条件得
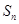 的表达式,根据通项
的表达式,根据通项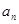 与前
与前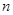 项和
项和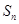 的关系:
的关系: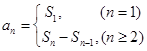 求出通项公式,再根据数列
求出通项公式,再根据数列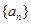 是等比数列,求出
是等比数列,求出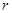 的值.
的值.(Ⅱ)要求和,先看通项.数列
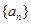 是等比数列,数列
是等比数列,数列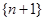 是等差数列,所以数列
是等差数列,所以数列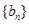 是差比型数列,因此使用错位相减法求和.
是差比型数列,因此使用错位相减法求和.试题分析:(Ⅰ)
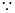 点
点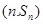 均在函数
均在函数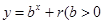 且
且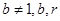 均为常数)的图像上,
均为常数)的图像上,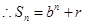 .
.当
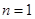 时,
时,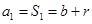 ;当
;当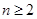 时,
时,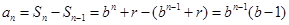
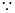 数列
数列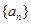 是等比数列,
是等比数列, 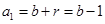 ,
,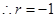 .
.(Ⅱ)当
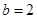 时,由(Ⅰ)知
时,由(Ⅰ)知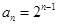 ,
,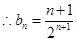 ,
,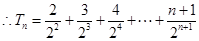 ,
, 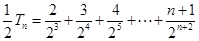 ,
,两式相减得
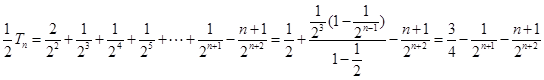
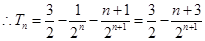
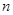 项和公式求通项公式;2.错位相减法求和.
项和公式求通项公式;2.错位相减法求和.
练习册系列答案
相关题目
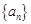 满足:
满足: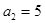 ,
,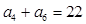 .
.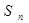 .
.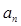 及
及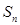 ;
;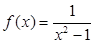 ,
,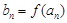 (
(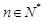 ),求数列
),求数列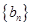 的前
的前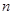 项和
项和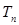 .
. 的前
的前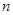 项和
项和 ,则
,则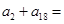 ( )
( )



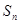 ,若
,若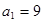 ,
,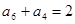 , 则当
, 则当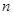 等于( )
等于( ) 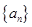 的公差
的公差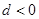 ,若
,若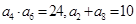 ,则该数列的前
,则该数列的前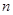 项和
项和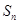 的最大值是( )
的最大值是( )
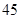
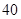
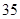
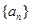 中,
中,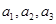 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且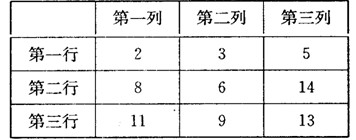
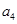 的值为( )
的值为( )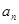 }满足
}满足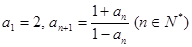 ,则
,则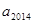 的值为 .
的值为 .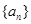 的前
的前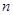 项和为
项和为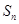 ,若
,若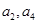 是方程
是方程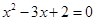 的两个实数根,则
的两个实数根,则 .
.