题目内容
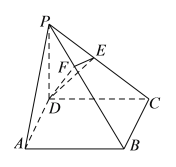
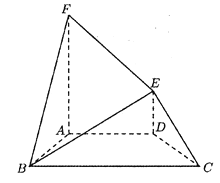
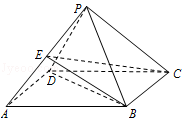
【题目】已知四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 
(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P﹣BCE的体积.
【答案】证明:(I)连接AC交BD于O点, 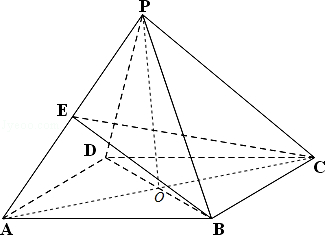
∵四边形ABCD是菱形,∴AC⊥BD,O是BD的中点,
∵PB=PD,∴PO⊥BD,
又AC∩OP=O,AC平面PAC,OP平面PAC,
∴BD⊥平面PAC,又PC平面PAC,
∴BD⊥PC.
(II)∵四边形ABCD是菱形,∠BAD=60°,
∴BD=AB=AD=2,∴OB=1,OA= ![]() ,
,
∴OP= ![]() =
= ![]() ,∴OA2+OP2=PA2 , 即OA⊥OP.
,∴OA2+OP2=PA2 , 即OA⊥OP.
∴S△PCE= ![]() S△PAC=S△POA=
S△PAC=S△POA= ![]() ×
× ![]() =
= ![]() .
.
∴又OB⊥平面PAC,
∴VP﹣BCE=VB﹣PCE= ![]() S△PCEOB=
S△PCEOB= ![]() ×1=
×1= ![]() .
.
【解析】(I)连接AC交BD于O点,由BD⊥AC,BD⊥OP得出BD⊥平面PAC,故PC⊥BD;(II)利用勾股定理计算OA,OP,证明OA⊥OP,得出三角形PCE的面积,于是VP﹣BCE=VB﹣PCE= ![]() S△PCEOP.
S△PCEOP.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目