题目内容
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高,然而也有部分公众对该活动的实际效果与负面影响提出了疑问,对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8个人打出的分数看作一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
(Ⅰ)100;(Ⅱ)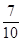 ;(Ⅲ)
;(Ⅲ)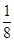 .
.
解析试题分析:(Ⅰ)根据分层抽样法的定义得比例关系易得所求值;(Ⅱ)先利用分层抽样法得5人中20岁以下和以上的人数分别为2、3,再分别记作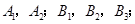 列出从中任取2人的所有事件,找出其中至少有1人20岁以下的基本事件,从而易得概率;(Ⅲ)先计算总体平均数,再找出与总体平均数之差的绝对值超过0.6的数,从而得概率.
列出从中任取2人的所有事件,找出其中至少有1人20岁以下的基本事件,从而易得概率;(Ⅲ)先计算总体平均数,再找出与总体平均数之差的绝对值超过0.6的数,从而得概率.
试题解析:(Ⅰ)由题意得,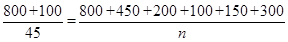 ,
,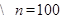 . 2分
. 2分
(Ⅱ)设所抽取的5人中,有m人20岁以下,则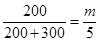 ,解之得
,解之得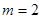 , 4分
, 4分
也就是20岁以下抽取了2人另一部分抽取了3人,分别记作: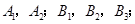 5分
5分
则从中任取2人的所有基本事件为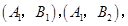
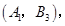
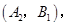
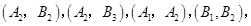
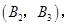
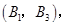 共10个, 7分
共10个, 7分
其中至少有1人20岁以下的基本事件有7个:
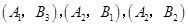
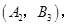
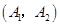 ,所以从中任意抽取2人,至少有1人20岁以下的概率为
,所以从中任意抽取2人,至少有1人20岁以下的概率为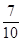 . 9分
. 9分
(Ⅲ)总体平均数为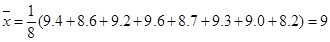 , 10分
, 10分
那么与总体平均数之差的绝对值超过0.6的数只有8.2, 11分
所以该数与总体平均数之差的绝对值超过0.6的概率为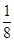 . 12分
. 12分
考点:1、分层抽样法;2、概率.

 智能训练练测考系列答案
智能训练练测考系列答案随着工业化的发展,环境污染愈来愈严重.某市环保部门随机抽取60名市民对本市空气质量满意度打分,把数据分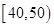 、
、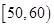 、
、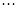 、
、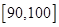 六段后得到如下频率分布表:
六段后得到如下频率分布表:
| 分组 | 频数 | 频率 |
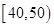 |  | 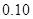 |
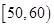 | 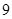 | 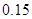 |
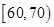 | 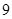 | 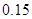 |
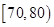 |  |  |
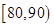 |  | 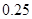 |
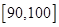 |  | 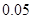 |
| 合计 | 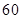 |  |
 、
、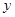 、
、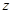 的值;
的值;(2)用分层抽样的方法在分数
 的市民中抽取容量为
的市民中抽取容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人在分数段
人在分数段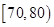 的概率.
的概率. 某种产品的广告费支出 与销售额
与销售额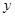 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
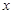 | 2 | 4 | 5 | 6 | 8 |
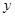 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:
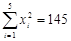


参考公式:线性回归方程系数:
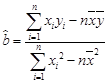 ,
, )
) 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):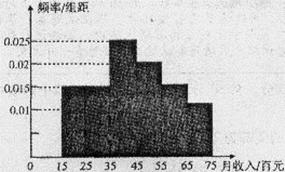
| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 1 |
(I)试根据频率分布直方图估计这60人的平均月收入;
(Ⅱ)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望.
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x | 15 | 20 | 25 | 30 |
| 水稻产量y | 330 | 345 | 365 | 405 |
(2)请估计当施化肥量为10时,水稻产量为多少?
(已知:7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125)

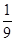 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.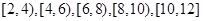 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
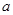 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;