题目内容
某种产品的广告费支出 与销售额
与销售额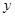 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
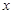 | 2 | 4 | 5 | 6 | 8 |
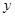 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:
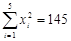


参考公式:线性回归方程系数:
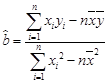 ,
, )
)
(1)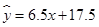 (2)销售收入大约为82.5万元(3)
(2)销售收入大约为82.5万元(3)
解析试题分析:(1)首先求出x,y的平均数,利用最小二乘法做出线性回归方程的系数,根据样本中心点满足线性回归方程,代入已知数据求出a的值,写出线性回归方程.(2)当自变量取10时,把10代入线性回归方程,求出销售额的预报值,这是一个估计数字,它与真实值之间有误差.(3)利用列举法计算基本事件数及事件发生的概率 .本题考查回归分析的初步应用,考查求线性回归方程,考查预报y的值,是一个综合题目,解此类题,关键是理解线性回归分析意义,这种题目是新课标的大纲要求掌握的题型,是一个典型的题目,在近年的高考中频率有增高的趋势,此类题运算量大,解题时要严谨防止运算出错.
试题解析:(1)解: ,
,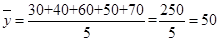 [2分]
[2分]
又已知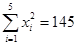 ,
,
于是可得: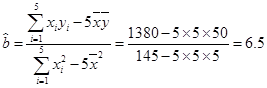 , [4分]
, [4分]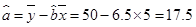 因此,所求回归直线方程为:
因此,所求回归直线方程为: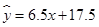 [6分]
[6分]
(2)解:根据上面求得的回归直线方程,当广告费支出为10万元时,
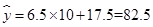 (万元) 即这种产品的销售收入大约为82.5万元. [9分]
(万元) 即这种产品的销售收入大约为82.5万元. [9分]
(3)解:
基本事件:(30,40),(30,60),(30,50),(30,70),(40,60),(40,50),(40,70),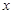
2 4 5 6 8 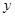
 30
3040 60 50 70 
30.5 43.5 50 56.5 69.5
(60,50),(60,70),(50,70)共10个
两组数据其预测值与实际值之差的绝对值都超过5:(60,50) [12分]
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为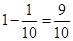 [14分]
[14分]
考点:1.回归分析的初步应用;2.列举法计算基本事件数及事件发生的概率

空气质量指数 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重. 的浓度与空气质量类别的关系如下表所示:
的浓度与空气质量类别的关系如下表所示:
 日均浓度 日均浓度 |  |  |  |  |  |  |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
天的 日均浓度指数数据茎叶图如图5所示.
日均浓度指数数据茎叶图如图5所示.
(1)试估计甲城市在
 年
年 月份的
月份的 天的空气质量类别为优或良的天数;
天的空气质量类别为优或良的天数;(2)在甲城市这
 个监测数据中任取
个监测数据中任取 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求 的分布列及数学期望.
的分布列及数学期望. 由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高,然而也有部分公众对该活动的实际效果与负面影响提出了疑问,对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8个人打出的分数看作一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
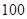 分,规定测试成绩在
分,规定测试成绩在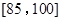 之间为体质优秀;在
之间为体质优秀;在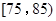 之间为体质良好;在
之间为体质良好;在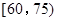 之间为体质合格;在
之间为体质合格;在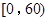 之间为体质不合格.
之间为体质不合格.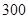 名学生中随机抽取
名学生中随机抽取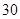 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下: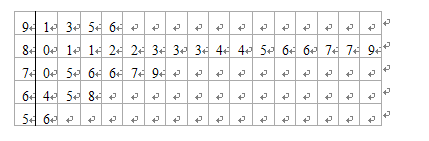
 名学生,再从这
名学生,再从这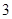 人.
人. 名体质为优秀的概率;
名体质为优秀的概率;
 ,求甲通过初赛的概率.
,求甲通过初赛的概率.


 ,求
,求
 .
.
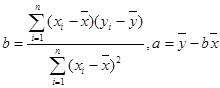 )
)