题目内容

连接双曲线
x2
a2
-
y2
b2
=1与
y2
b2
-
x2
a2
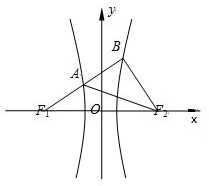
=1的四个顶点构成的四边形的面积为S1，连接它们的四个焦点构成的四边形的面积为S2，则S1：S2的最大值是（　　）
A．2B．1C．
1
2
D．
1
4
设双曲线
x2
a2
-
y2
b2
=1的右顶点为A，其坐标是（a，0），由焦点为C，坐标为（
a2+b2
，0）；
设双曲线
y2
b2
-
x2
a2
=1上顶点为B，坐标为（0，b），上焦点为D，坐标为（0，
a2+b2
）．O为坐标原点．
则S1=4S△OAB=2ab，S2=4S△OCD=2（a2+b2），
所以
S1
S2
=
ab
a2+b2
≤
ab
2ab
=
1
2
．
故选C．
练习册系列答案
相关题目
【文科】若双曲线的渐近线方程为y=±3x，一个焦点是(0，
10
)，则双曲线的方程是______．
过双曲线2x2-y2-2=0的右焦点作直线l交曲线于A、B两点，若|AB|=2则这样的直线存在（　　）
A．0条B．1条C．2条D．3条
若双曲线以y=±2x为渐近线，且A（1，0）为一个顶点，则双曲线的方程为（　　）
A．
x2
4
-y2=1		B．y2-
x2
4
=1		C．x2-
y2
4
=1		D．
y2
4
-x2=1
如图，F1，F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，过F1的直线l与C的左、右分支分别交于A，B两点．若AB：BF2：AF2=3：4：5，则双曲线的离心率为______．
双曲线
x2
9
-
y2
4
=1的渐近线方程是（　　）
A．y=±
2
3
x		B．y=±
3
2
x		C．y=±
4
9
x		D．y=±
9
4
x
双曲线的方程为
x2
16
-
y2
9
=1，则其离心率为（　　）
A．
4
5
B．
5
4
C．±
4
5
D．±
5
4
双曲线
x2
4
-
y2
25
=1的渐近线方程是（　　）
A．y=±
25
4
x		B．y=±
4
25
x		C．y=±
5
2
x		D．y=±
2
5
x
双曲线y2-3x2=9的渐近线方程是（　　）
A．y=±3xB．y=±
1
3
x		C．y=±
3
x		D．y=±
3
3
x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网