题目内容
10.设函数f(x)=ax2+bx+c(a≠0),曲线y=f(x)通过点(0,2a+3),且在点(-1,f(-1))处的切线垂直于y轴.(1)用a分别表示b和c;
(2)讨论函数g(x)=-f(x)•e-x的单调性;
(3)当a=-3时,若对任意的x1,x2∈[-2,+∞),不等式|g(x1)-g(x2)≤M恒成立,求M的最小值.
分析 (1)把(0,2a+3)代入到f(x)的解析式中得到c与a的解析式,解出c;求出f′(x),因为在点(-1,f(-1))处的切线垂直于y轴,得到切线的斜率为0,即f′(-1)=0,代入导函数得到b与a的关系式,解出b即可.
(2)由(1)得,f(x)=ax2+2ax+2a+3,利用导数法分类讨论,可得不同情况下,函数g(x)=-f(x)•e-x的单调性;
(3)当a=-3时,由(2)得函数的单调性,进而求出函数的最值,可得M的范围,进而得到M的最小值.
解答 解:(1)由f(x)=ax2+bx+c得到f'(x)=2ax+b.
因为曲线y=f(x)通过点(0,2a+3),故f(0)=c=2a+3,
又曲线y=f(x)在(-1,f(-1))处的切线垂直于y轴,故f′(-1)=0,
即-2a+b=0,因此b=2a.
(2)由(1)得f(x)=ax2+2ax+2a+3,
∴g(x)=-f(x)•e-x=-$\frac{{ax}^{2}+2ax+2a+3}{{e}^{x}}$,
∴g′(x)=$\frac{{ax}^{2}+3}{{e}^{x}}$,
当a>0时,g′(x)>0恒成立,函数g(x)=-f(x)•e-x在R上单调递增;
当a<0时,令g′(x)=0,则x=±$\sqrt{-\frac{3}{a}}$,
当x∈(-∞,-$\sqrt{-\frac{3}{a}}$)时,g'(x)<0,故g(x)在x∈(-∞,-$\sqrt{-\frac{3}{a}}$)上为减函数;
当x∈(-$\sqrt{-\frac{3}{a}}$,$\sqrt{-\frac{3}{a}}$)时,g'(x)>0,故g(x)在x∈(-$\sqrt{-\frac{3}{a}}$,$\sqrt{-\frac{3}{a}}$)上为增函数.
当x∈($\sqrt{-\frac{3}{a}}$,+∞)时,g'(x)<0,故g(x)在x∈($\sqrt{-\frac{3}{a}}$,+∞)上为减函数;
(3)当a=-3时,由(2)得:
g(x)在x∈(-∞,-1)上为减函数;在(-1,1)上为增函数;在(1,+∞)上为减函数;
∵x∈[-2,+∞)时,
∴当x=-2时,函数取最大值3e,当x=-1时,函数取最小值0,
若对任意的x1,x2∈[-2,+∞),不等式|g(x1)-g(x2)|≤M,
则M≥3e,
即M的最小值为3e.
点评 本题是一道综合题,要求学生会利用导数研究函数的单调性,会利用导数研究曲线上某点的切线方程.做题时注意复合函数的求导法则.

 黄冈创优卷系列答案
黄冈创优卷系列答案| A. | (-∞,-4)∪(6,+∞) | B. | [-4,6] | C. | (-4,6) | D. | (-6,4) |
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{\sqrt{29}}{4}$ |
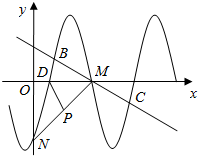 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).