题目内容
【题目】已知命题p:x∈(1,+∞), ![]() >1;命题q:a∈(0,1),函数y=ax在(﹣∞,+∞)上为减函数,则下列命题为真命题的是( )
>1;命题q:a∈(0,1),函数y=ax在(﹣∞,+∞)上为减函数,则下列命题为真命题的是( )
A.p∧q
B.¬p∧q
C.p∧¬q
D.¬p∧¬q
【答案】A
【解析】 解:命题p:x∈(1,+∞),由幂函数的性质可得 ![]() >1,是真命题;
>1,是真命题;
命题q:a∈(0,1),函数y=ax在(﹣∞,+∞)上为减函数,利用指数函数的单调性可知:是真命题.
则下列命题为真命题的是p∧q,其余的为假命题.
故选;A.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.

练习册系列答案
相关题目
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)用所求回归方程预测该地区2015年![]() 的人民币储蓄存款.
的人民币储蓄存款.
附:回归方程![]() 中,
中, 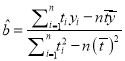 ,
,