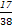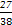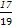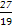题目内容
已知关于x的二次函数f(x)＝ax2－4bx＋1.设集合P＝{－1，1，2，3，4，5}和Q＝{－2，－1，1，2，3，4}，分别从集合P和Q中任取一个数作为a和b的值，则函数y＝f(x)在区间[1，＋∞)上是增函数的概率为________．
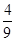
函数f(x)＝ax2－4bx＋1图象的对称轴为x＝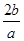
.要使y＝f(x)在区间[1，＋∞)上为增函数，应有a>0且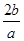≤1，∴ a≥2b且a>0.
① 若a＝1，则b＝－2，－1；② 若a＝2，则b＝－2，－1，1；③ 若a＝3，则b＝－2，－1，1；④ 若a＝4，则b＝－2，－1，1，2；⑤ 若a＝5，则b＝－2，－1，1，2，∴ 该事件包含基本事件数为16，所求概率P＝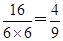
.
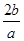.要使y＝f(x)在区间[1，＋∞)上为增函数，应有a>0且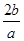≤1，∴ a≥2b且a>0.① 若a＝1，则b＝－2，－1；② 若a＝2，则b＝－2，－1，1；③ 若a＝3，则b＝－2，－1，1；④ 若a＝4，则b＝－2，－1，1，2；⑤ 若a＝5，则b＝－2，－1，1，2，∴ 该事件包含基本事件数为16，所求概率P＝
.
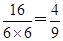练习册系列答案
手拉手全优练考卷系列答案
相关题目
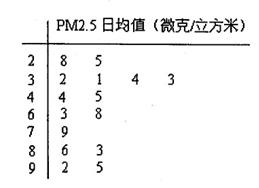
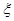表示空气质量达到一级的天数，求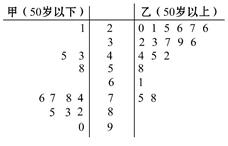
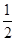，P(B)＝
，则出现奇数点或2点的概率为________．
，
.
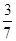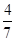)i,i=1,2,3,则a的值是( )
