题目内容
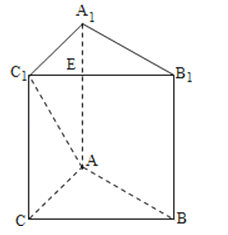
【题目】如图，在四面体
中，平面
平面
， 
， 
， 
分别为
， 
， 
的中点， 
， 
.
（1）求证： 
平面
；
（2）若
为
上任一点，证明
平面
.
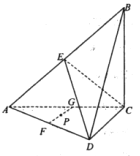
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）先由面面垂直性质定理得
平面
，即得
，再根据等腰三角形性质得
，最后根据线面垂直判定定理得
平面
.（2）实质要证明面面平行：平面
平面
，先根据线线平行得线面平行： 
平面
及
平面
，，再根据线面平行得面面平行
试题解析：解：（1）因为平面
平面
， 
，即
，
平面
平面
， 
平面
，
所以
平面
，
又
平面
，所以
，
因为
， 
为
的中点，所以
，
又
， 
平面
， 
平面
，
所以
平面
.
（2）连
， 
，因为
， 
分别为
， 
的中点，
所以
，又
平面
， 
平面
，
所以
平面
，
同理可证
平面
，且
， 
平面
， 
平面
，
所以平面
平面
，
又
为
上任一点，所以
平面
，所以
平面
.
练习册系列答案
相关题目
【题目】（本题满分10分）已知等差数列{an}满足a1＋a2＝10，a4－a3＝2.
(1)求{an}的通项公式．
(2)设等比数列{bn}满足b2＝a3，b3＝a7.问：b6与数列{an}的第几项相等？
