题目内容
【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
【答案】
(1)解:由x2﹣3x+2=0得x=1或x=2,故集合A={1,2}
∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0a=﹣1或a=﹣3;
当a=﹣1时,B={x|x2﹣4=0}={﹣2,2},满足条件;
当a=﹣3时,B={x|x2﹣4x+4=0}={2},满足条件;
综上,a的值为﹣1或﹣3
(2)解:对于集合B,
△=4(a+1)2﹣4(a2﹣5)=8(a+3).
∵A∪B=A,∴BA,
①当△<0,即a<﹣3时,B=满足条件;
②当△=0,即a=﹣3时,B={2},满足条件;
③当△>0,即a>﹣3时,B=A={1,2}才能满足条件,
则由根与系数的关系得
![]()
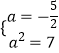 矛盾;
矛盾;
综上,a的取值范围是a≤﹣3
【解析】(1)先解出集合A,根据2是两个集合的公共元素可知2∈B,建立关于a的等式关系,求出a后进行验证即可.(2)一般A∪B=A转化成BA来解决,集合A两个元素故可考虑对集合B的元素个数进行讨论求解.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
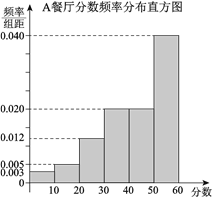
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
