题目内容
20.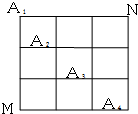 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.(Ⅰ)求甲由M处到达N处的不同走法种数;
(Ⅱ)求甲经过A2的概率.
分析 (Ⅰ),甲由道路网M处出发随机地选择一条沿街的最短路径到达N处需走6步,共有$C_6^3$种,问题得以解决.
(Ⅱ)本题是一个等可能事件的概率,试验发生包含的事件是C63,满足条件的事件是甲经过A2到达N,可分为两步:甲从M经过A2的方法数C31种;甲从A2到N的方法数C31种;根据分步计数原理得到结果数,求出概率.
解答 解:(Ⅰ)甲由道路网M处出发随机地选择一条沿街的最短路径到达N处需走6步,共有$C_6^3$种,即共有20种.
(Ⅱ)甲经过A2到达N,可分为两步:第一步:甲从M经过A2的方法数:$C_3^1$种;
第二步:甲从A2到N的方法数:$C_3^1$种;所以:甲经过A2的方法数为${(C_3^1)^2}$=9种,
所以:甲经过A2的概率$P=\frac{{{{(C_3^1)}^2}}}{C_6^3}=\frac{9}{20}$.
点评 本题考查等可能事件的概率,考查分类计数原理,考查分步计数原理,是一个综合题.

练习册系列答案
相关题目
 一小车A从静止开始以2m/s2的加速度作匀加速度直线运动,持续5秒钟后作加速度为0的匀速直线运动,并保持10秒,最后以-1m/s2的加速度作匀减速度直线运动直至小车静止.另有一小车B在同一起点,从开始时刻以速度v0作匀速直线运动.
一小车A从静止开始以2m/s2的加速度作匀加速度直线运动,持续5秒钟后作加速度为0的匀速直线运动,并保持10秒,最后以-1m/s2的加速度作匀减速度直线运动直至小车静止.另有一小车B在同一起点,从开始时刻以速度v0作匀速直线运动.