题目内容
12.定义若数列{an}对任意的正整数n,都有|an-1|+|an|=d(d为常数)则称{an}为“绝对和数列”,d叫做“绝对公和”,已知“绝对和数列”{an}中,a1=2,绝对公和为3,则其前2009项的和s2009的最小值为( )| A. | -2009 | B. | -3010 | C. | -3014 | D. | 3028 |
分析 通过写出前几项的值可知满足条件的数列{an}的通项公式,进而利用分组法求和计算即得结论.
解答 解:依题意,要使其前2009项的和S2009的最小值只需每一项的值都取最小值即可,
∵a1=2,绝对公和d=3,
∴a2=-1或a2=1(舍),
∴a3=-2或a3=2(舍),
∴a4=-1或a4=1(舍),
…
∴满足条件的数列{an}的通项公式an=$\left\{\begin{array}{l}{2,}&{n=1}\\{-2,}&{n为大于1的奇数}\\{-1,}&{n为偶数}\end{array}\right.$,
∴所求值为a1+(a2+a3)+(a4+a5)+…+(a2008+a2009)
=2+(-1-2)×$\frac{2009-1}{2}$
=-3010,
故选:B.
点评 本题考查考查数列的求和,找出满足条件的数列的通项公式是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.某品牌电视专卖店,在“五一”期间设计一项有奖促销活动:每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,产生20组随机数组,每组3个数,试验结果如下所示:
975,146,858,513,277,645,903,756,111,783,
834,527,060,089,221,368,054,669,863,175.
(Ⅰ)请根据以上模拟数据估计:若活动期间商家卖出100台电视应付出奖金多少元?
(Ⅱ)在以上模拟数据的前5组数中,随机抽取2组数,试写出所有的基本事件,并求至少有一组获奖的概率.
| 随机数组的特征 | 3个数字均相同 | 恰有2个数字相同 | 其余情况 |
| 奖金(单位:元) | 500 | 200 | 0 |
975,146,858,513,277,645,903,756,111,783,
834,527,060,089,221,368,054,669,863,175.
(Ⅰ)请根据以上模拟数据估计:若活动期间商家卖出100台电视应付出奖金多少元?
(Ⅱ)在以上模拟数据的前5组数中,随机抽取2组数,试写出所有的基本事件,并求至少有一组获奖的概率.
17.函数f(x)=∫${\;}_{0}^{x}$t(t-4)dt在[-1,5]上( )
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
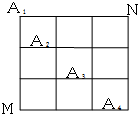 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处. 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.