题目内容
10.已知cos(α-55°)=-$\frac{1}{3}$,且α为第四象限角,求sin(α+125°)的值.分析 由条件利用同角三角函数的基本关系求得sin(α-55°)的值,再利用诱导公式求得sin(α+125°)的值.
解答 解:∵cos(α-55°)=-$\frac{1}{3}$,且α为第四象限角,
∴α-55°为第三象限角,∴sin(α-55°)=-$\sqrt{{1-cos}^{2}(α-55°)}$=-$\frac{2\sqrt{2}}{3}$.
∴sin(α+125°)=sin(α-55°+180°)=-sin(α-55°)=$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查同角三角函数的基本关系,诱导公式的应用,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
15. 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |
19.如果把函数y=$\frac{1}{4}$sin2x的图象按向量$\overrightarrow{v}$平移,就可以得到函数y=$\frac{1}{4}$sin(2x-$\frac{π}{3}$)的图象,那么向量$\overrightarrow{v}$的坐标是( )
| A. | ($\frac{π}{3}$,0) | B. | ($\frac{π}{6}$,0) | C. | (-$\frac{π}{3}$,0) | D. | (-$\frac{π}{6}$,0) |
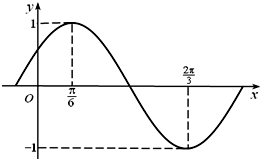 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.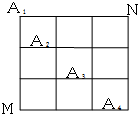 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.