题目内容
【题目】已知函数y=|x2﹣1|的图象与函数y=kx2﹣（k+2）x+2的图象恰有2个不同的公共点，则实数k的取值范围为 ．
【答案】k≤0或k=1或k≥4
【解析】解：函数y=kx2﹣（k+2）x+2=（kx﹣2）（x﹣1）的图象与函数y=|x2﹣1|的图象有1个交点（1，0）．
当k＜0， 
，函数y=|x2﹣1|的图象与函数y=kx2﹣（k+2）x+2的图象有另外1个不同于（1，0）的交点；
由1﹣x2=kx2﹣（k+2）x+2，（x﹣1）[（k+1）x﹣1]=0，x=1时，k=0，方程有唯一的根1，
满足函数y=|x2﹣1|的图象与函数y=kx2﹣（k+2）x+2的图象
恰有2个不同的公共点；
k＞0时，由图象可得k=1或k≥4满足题意，
综上所述，k≤0或k=1或k≥4．
所以答案是：k≤0或k=1或k≥4．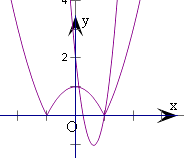
【考点精析】通过灵活运用二次函数的性质，掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减即可以解答此题．
练习册系列答案
相关题目
