题目内容
【题目】三个圆交于一点
，又两两将于点
、
、
.以为圆心的一个圆
与上述三个圆分别交于点
，
，
，其中，点在不含点的圆上，等等.又设
、
、
的外接圆交于一点
，
、
的外接圆交于一点
.证明：
.
【答案】见解析
【解析】
以圆
为基圆作反演，各点反演后的像仍用同一字母表示（下面出现的字母都是各点反演后的像）.则三个圆的反形为三条直线
、
、
（如图）.
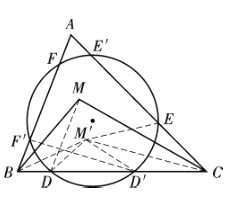
只需证明反形中有
.
由条件，反演后
仍为
、
、
的外接圆的交点，
仍为
、
、
的外接圆的交点.
首先证明：是点的等角共轭点（即
等）.
事实上，
.
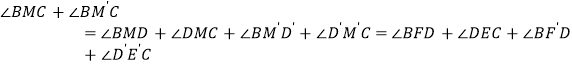
设的等角共轭点为
.则
.
所以，
.
类似得到其他两式.
于是，
.
其次，作，关于
的垂足三角形
、
（图）.
因
，所以，
、
、
、
四点共圆.
同样得到另两个圆.
若这三个圆不重合，则其三条根轴（
、
、
）共点，此时，三边共点，矛盾.
于是这三个圆重合，即、、、、
、
六点共圆，设其圆心为
，则在、、的中垂线上，这些中垂线平分
的中点.
由共圆知，
.
则
.
绕点旋转角度
，再作以为中心的相似变换，使相似比为
.
则
，
.
所以，
.
显然，
.
故
.
又为的中点，故.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
