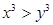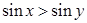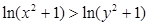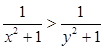题目内容
已知函数f(x)=2x,g(x)=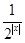 +2.
+2.
(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
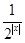 +2.
+2.(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
(1)(2,3] (2)log2(1+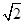 )
)
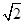 )
)解:(1)g(x)=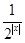 +2=(
+2=(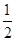 )|x|+2,
)|x|+2,
因为|x|≥0,所以0<(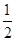 )|x|≤1,
)|x|≤1,
即2<g(x)≤3,故g(x)的值域是(2,3].
(2)由f(x)-g(x)=0,
得2x-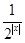 -2=0,
-2=0,
当x≤0时,显然不满足方程,
即只有x>0时满足2x-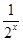 -2=0,
-2=0,
整理得(2x)2-2·2x-1=0,(2x-1)2=2,故2x=1±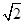 ,
,
因为2x>0,所以2x=1+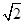 ,
,
即x=log2(1+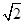 ).
).
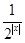 +2=(
+2=(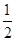 )|x|+2,
)|x|+2,因为|x|≥0,所以0<(
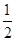 )|x|≤1,
)|x|≤1,即2<g(x)≤3,故g(x)的值域是(2,3].
(2)由f(x)-g(x)=0,
得2x-
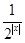 -2=0,
-2=0,当x≤0时,显然不满足方程,
即只有x>0时满足2x-
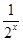 -2=0,
-2=0,整理得(2x)2-2·2x-1=0,(2x-1)2=2,故2x=1±
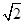 ,
,因为2x>0,所以2x=1+
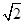 ,
,即x=log2(1+
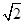 ).
).
练习册系列答案
相关题目
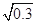 ,b=
,b=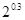 ,
,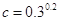 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )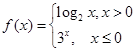 ,且函数
,且函数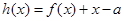 有且只有一个零点,则实数
有且只有一个零点,则实数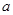 的取值范围是( )
的取值范围是( )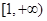 B.
B.
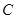 .
.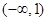 D.
D.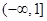
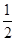 },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )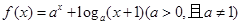 在区间
在区间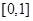 上的最大值与最小值的和为
上的最大值与最小值的和为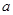 ,则实数
,则实数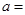 ___ ___.
___ ___.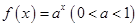 在区间[0,2]上的最大值比最小值大
在区间[0,2]上的最大值比最小值大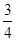 ,则
,则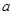 的值为( )
的值为( )



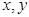 满足
满足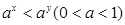 ,则下列关系式恒成立的是( )
,则下列关系式恒成立的是( )