题目内容
某公司生产某种消防安全产品,年产量x台(0≤x≤100,x∈N)时,销售收入函数R(x)=3000x-20x2(单位:百元),其成本函数满足C(x)=500x+b(单位:百元).已知该公司不生产任何产品时,其成本为4000(百元).
(1)求利润函数P(x);
(2)问该公司生产多少台产品时,利润最大,最大利润是多少?
(3)在经济学中,对于函数f(x),我们把函数f(x+1)-f(x)称为函数f(x)的边际函数,记作Mf(x).对于(1)求得的利润函数P(x),求边际函数MP(x);并利用边际函数MP(x)的性质解释公司生产利润情况.(本题所指的函数性质主要包括:函数的单调性、最值、零点等)
解:(1)由题意,x=0,b=4000,
所以C(x)=500x+4000,
P(x)=R(x)-C(x)=3000x-20x2-500x-4000
=-20x2+2500x-4000,0≤x≤100.
(2)P(x)=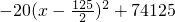 ,(0≤x≤100,x∈N)
,(0≤x≤100,x∈N)
所以x=62或x=63.
P(x)max=P(62)=P(63)=74120(百元).
(3)MP(x)=P(x+1)-P(x)=-40x+2480(0≤x≤99,x∈N)
边际函数为减函数,说明随着产量的增加,每生产一台的利润与生产前一台利润相比在减少;
当x=0时,边际函数取得最大值为2480,说明生产第一台的利润差最大;
当x=62时,边际函数为零,说明生产62台时,利润达到最大.
分析:(1)由题意,x=0,b=4000,所以C(x)=500x+4000,P(x)=R(x)-C(x)=3000x-20x2-500x-4000=-20x2+2500x-4000,0≤x≤100.
(2)P(x)=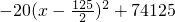 ,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.
,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.
(3)MP(x)=P(x+1)-P(x)=-40x+2480(0≤x≤99,x∈N).边际函数为减函数,说明随着产量的增加,每生产一台的利润与生产前一台利润相比在减少;说明生产第一台的利润差最大;生产62台时,利润达到最大.
点评:本题考查函数在生产实际中的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
所以C(x)=500x+4000,
P(x)=R(x)-C(x)=3000x-20x2-500x-4000
=-20x2+2500x-4000,0≤x≤100.
(2)P(x)=
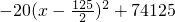 ,(0≤x≤100,x∈N)
,(0≤x≤100,x∈N)所以x=62或x=63.
P(x)max=P(62)=P(63)=74120(百元).
(3)MP(x)=P(x+1)-P(x)=-40x+2480(0≤x≤99,x∈N)
边际函数为减函数,说明随着产量的增加,每生产一台的利润与生产前一台利润相比在减少;
当x=0时,边际函数取得最大值为2480,说明生产第一台的利润差最大;
当x=62时,边际函数为零,说明生产62台时,利润达到最大.
分析:(1)由题意,x=0,b=4000,所以C(x)=500x+4000,P(x)=R(x)-C(x)=3000x-20x2-500x-4000=-20x2+2500x-4000,0≤x≤100.
(2)P(x)=
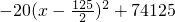 ,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.
,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.(3)MP(x)=P(x+1)-P(x)=-40x+2480(0≤x≤99,x∈N).边际函数为减函数,说明随着产量的增加,每生产一台的利润与生产前一台利润相比在减少;说明生产第一台的利润差最大;生产62台时,利润达到最大.
点评:本题考查函数在生产实际中的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =(1,2),
=(1,2), =(x,2),则向量
=(x,2),则向量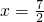
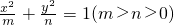 和双曲线
和双曲线 有相同焦点F1,F2,P是两曲线的公共点,则|PF1|•|PF2|的值是________.
有相同焦点F1,F2,P是两曲线的公共点,则|PF1|•|PF2|的值是________. ,n为正整数,则使 Tn最大的n的值为
,n为正整数,则使 Tn最大的n的值为 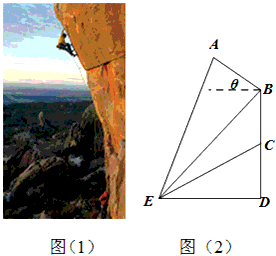 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求: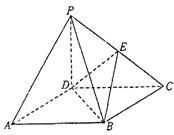 如图,四棱锥P-ABCD的底面ABCD是正方形,
如图,四棱锥P-ABCD的底面ABCD是正方形,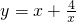
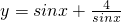 (0<x<π)
(0<x<π)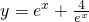
 的值为
的值为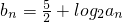 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn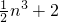 (n=1,2,3…)的大小,并说明理由.
(n=1,2,3…)的大小,并说明理由.