题目内容
记数列{an}前n项的积为πn=a1a2…an,设 Tn=π1π2…πn.若数列 ,n为正整数,则使 Tn最大的n的值为
,n为正整数,则使 Tn最大的n的值为
- A.11
- B.22
- C.25
- D.48
B
分析:先求πn=a1a2…an,再求 Tn=π1π2…πn.进而可求Tn最大的n的值.
解答:由题意,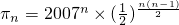 ,∴
,∴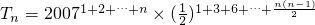 ,
,
从而可求 Tn最大的n的值为22,
故选B.
点评:本题的考点是数列的函数特性,主要课程新定义,考查数列的前n项的和,有一定的技巧.
分析:先求πn=a1a2…an,再求 Tn=π1π2…πn.进而可求Tn最大的n的值.
解答:由题意,
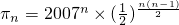 ,∴
,∴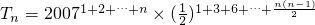 ,
,从而可求 Tn最大的n的值为22,
故选B.
点评:本题的考点是数列的函数特性,主要课程新定义,考查数列的前n项的和,有一定的技巧.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
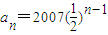 ,n为正整数,则使 Tn最大的n的值为 ( )
,n为正整数,则使 Tn最大的n的值为 ( )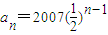 ,n为正整数,则使 Tn最大的n的值为 ( )
,n为正整数,则使 Tn最大的n的值为 ( )