题目内容
已知等比数列{an},Sn是其前n项的和,且a1+a3=5,S4=15.
(I)求数列{an}的通项公式;
(II)设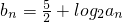 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn
(III)比较(II)中Tn与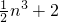 (n=1,2,3…)的大小,并说明理由.
(n=1,2,3…)的大小,并说明理由.
解:(I)设数列{an}的公比为q,则
方法一:a1+a3=a1+a1q2=a1(1+q2)=5,S4-(a1+a3)=a2+a4=a1q(1+q2)=10
∴q=2,a1=1,则an=2n-1
方法二:易知q≠1,则a1+a3=a1+a1q2=a1(1+q2)=5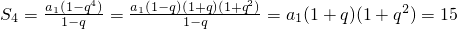 ,
,
则1+q=3
(以下同方法一)
(II)由(I)可得,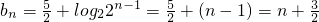 ,
,
所以数列{bn}是一个以 为首项,1为公差的等差数列
为首项,1为公差的等差数列
∴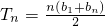
=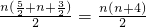
(III)∵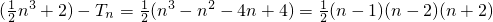
∴当n=1、2时,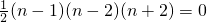 ,即Tn=
,即Tn=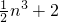
当n≥3时,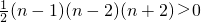 ,即Tn<
,即Tn<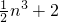
分析:(I)设{an}的公比为q,则由题意知a1+a3=a1+a1q2=a1(1+q2)=5,S4-(a1+a3)=a2+a4=a1q(1+q2)=10,由此可知an=2n-1.
(II)由题意知,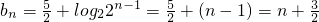 ,由此可知
,由此可知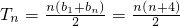 .
.
(III)由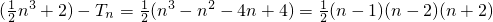 知当n=1、2时,Tn=
知当n=1、2时,Tn=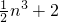 ;当n≥3时Tn<
;当n≥3时Tn<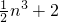 .
.
点评:本题考查数列的综合应用,解题时要注意审题,仔细解答.
方法一:a1+a3=a1+a1q2=a1(1+q2)=5,S4-(a1+a3)=a2+a4=a1q(1+q2)=10
∴q=2,a1=1,则an=2n-1
方法二:易知q≠1,则a1+a3=a1+a1q2=a1(1+q2)=5
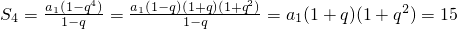 ,
,则1+q=3
(以下同方法一)
(II)由(I)可得,
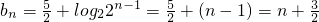 ,
,所以数列{bn}是一个以
 为首项,1为公差的等差数列
为首项,1为公差的等差数列∴
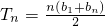
=
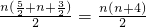
(III)∵
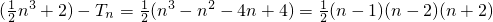
∴当n=1、2时,
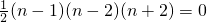 ,即Tn=
,即Tn=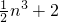
当n≥3时,
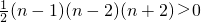 ,即Tn<
,即Tn<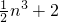
分析:(I)设{an}的公比为q,则由题意知a1+a3=a1+a1q2=a1(1+q2)=5,S4-(a1+a3)=a2+a4=a1q(1+q2)=10,由此可知an=2n-1.
(II)由题意知,
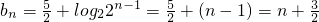 ,由此可知
,由此可知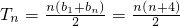 .
.(III)由
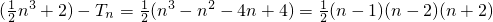 知当n=1、2时,Tn=
知当n=1、2时,Tn=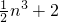 ;当n≥3时Tn<
;当n≥3时Tn<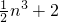 .
.点评:本题考查数列的综合应用,解题时要注意审题,仔细解答.

练习册系列答案
相关题目