题目内容
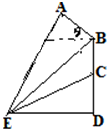
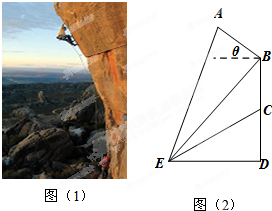
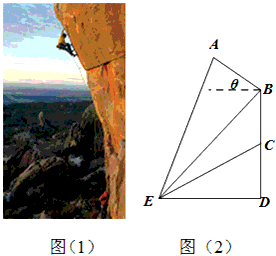 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
(1)BD间的距离及CD间的距离;
(2)在A处攀岩者距地面的距离h.
 解:(1)根据题意得∠CED=γ,∠ABE=β,∠AED=α
解:(1)根据题意得∠CED=γ,∠ABE=β,∠AED=α在直角三角形CED中,tanγ=
 ,CD=atanγ
,CD=atanγ在直角三角形BED中,tanγ=
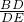 ,BD=atanβ
,BD=atanβ(2)由题意,AE=
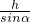 ,BE=
,BE=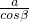
在△ABE中,∠AEB=α-β,∠EAB=π-(α+θ),
由正弦定理得:
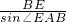 =
=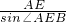
代入整理:
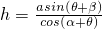 .
.分析:(1)根据题意得∠CED=γ,∠ABE=β,∠AED=α,借助图形分别在直角三角形CED和直角三角形BED中求解;
(2)在直角三角形中先求出AE,BE,然后在△ABE中利用正弦定理即可求得.
点评:本题考查学生利用直角三角形求解三角形中的知识,考查利用正弦定理求解三角形,属于中档题.

练习册系列答案
相关题目
 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=a,
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=a,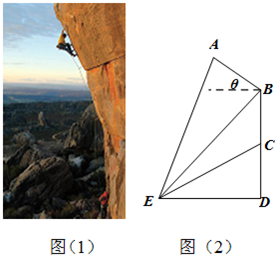 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
 分别为两名攀岩者所在位置,点
分别为两名攀岩者所在位置,点 为山的拐角处,且斜坡AB的坡角为
为山的拐角处,且斜坡AB的坡角为 ,点
,点 为山脚,某人在地面上的点
为山脚,某人在地面上的点 处测得
处测得 的仰角分别为
的仰角分别为 ,
,
 ,
,
 间的距离及点
间的距离及点 间的距离;
间的距离; 处攀岩者距地面的距离
处攀岩者距地面的距离 .
.