题目内容
下列函数中,在(0,+∞)上是减函数的是( )
| A、y=2x |
| B、y=-5x+3 |
| C、y=-x2+2x |
| D、y=log3x |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:考查四个选项,涉及到的函数为一次函数,二次函数,指数函数,对数函数,根据每个函数的特征依据其性质对其单调性作出判断,得正正确选项即可
解答:
解:A选项不正确,y=2x是增函数,
C、y=-x2+2x=-(x-1)2+1,此二次函数在区间(0,+∞)上不是减函数;
D选项不正确,由对数函数的底数大于1,故其在区间(0,+∞)上是增函数.
故选:B.
C、y=-x2+2x=-(x-1)2+1,此二次函数在区间(0,+∞)上不是减函数;
D选项不正确,由对数函数的底数大于1,故其在区间(0,+∞)上是增函数.
故选:B.
点评:本题考查函数的单调性的判断与证明,正确解答本题关键是对所涉及到的四个函数的单调性有着透彻的了解可以帮助快速作出判断.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
若a>b>0,则下列结论正确的是( )
| A、a2<b2 | ||
| B、ab<b2 | ||
C、a+b>2
| ||
| D、a-b>a+b |
已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B=( )
| A、(-1,4) |
| B、(-1,3) |
| C、(0,3) |
| D、(0,4) |
已知集合A={1,2,3},则下列结论正确的是( )
| A、0∈A | B、6∈A |
| C、2∉A | D、1∈A |
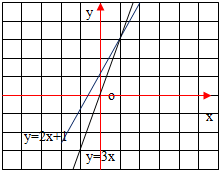 在同一坐标系中作出y=2x+1,y=3x的图象.
在同一坐标系中作出y=2x+1,y=3x的图象.