题目内容
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,点P在椭圆上,
,点P在椭圆上,![]() ,椭圆的离心率
,椭圆的离心率![]() .
.
(1)求椭圆C的标准方程;
(2)A,B是椭圆C上与点P不重合的任意两点,若![]() 的重心是坐标原点O,试证明:
的重心是坐标原点O,试证明:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
【答案】(1)![]() ;(2)证明详见解析,该定值为
;(2)证明详见解析,该定值为![]() .
.
【解析】
(1)根据待定系数法求出椭圆方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立方程组求出弦长
,联立方程组求出弦长![]() ,求出P到
,求出P到![]() 的距离,得出三角形的面积关于m的函数,从而得出面积的最大值.
的距离,得出三角形的面积关于m的函数,从而得出面积的最大值.
(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴椭圆C的标准方程为:![]() ;
;
(2)![]() 最多只有1条边所在直线与x轴垂直,
最多只有1条边所在直线与x轴垂直,
不妨设![]() 所在直线与x轴不垂直,其方程为
所在直线与x轴不垂直,其方程为![]()
(∵![]() 的重心是O,∴O不在直线
的重心是O,∴O不在直线![]() 上,
上,![]() )
)
由 得,
得,![]()
设![]() 、
、![]() ,则
,则
![]() ,
,
且![]() ,
,![]() ,
,
从而![]() ,
,
设![]() ,∵
,∵![]() 的重心是坐标原点O,
的重心是坐标原点O,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
点![]() 在椭圆
在椭圆![]() 上,
上,
∴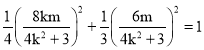
即![]() ,且符合
,且符合![]() ,
,
点![]() 到直线
到直线![]() 的距离为:
的距离为:
![]() ,
,
![]() 的面积
的面积![]() ,
,
由![]() 即
即![]() ,得
,得
![]() 为常数.
为常数.

练习册系列答案
相关题目