题目内容
17. 如图,在Rt△AOB中,∠OAB=(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)求异面直线AO与CD所成角的大小.
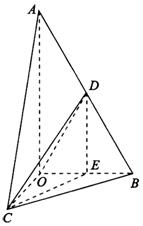
解法一:
(Ⅰ)由题意,CO⊥AO,BO⊥AO,
∴∠BOC是二面角B-AO-C的平面角.
又∵二面角B-AO-C是直二面角,
∴CO⊥BO,又∵AO∩BO=O,
∴CO⊥平面AOB,
又CO![]() 平面COD,
平面COD,
∴平面COD⊥平面AOB.
(Ⅱ)作DE⊥OB,垂足为E,连结CE(如图),则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.
在Rt△COE中,CO=BO=2,OE=![]() BO=1,
BO=1,
∴CE=![]() .
.
又DE=![]() AO=
AO=![]() ,
,
∴在Rt△CDE中,tan∠CDE=![]() ,
,
∴异面直线AO与CD所成角的大小为arctan![]() .
.

解法二:
(Ⅰ)同解法一.
(Ⅱ)建立空间直角坐标系O-xyz,如图,
则O(0,0,0),A(0,0,2![]() ),C(2,0,0),D(0,1,
),C(2,0,0),D(0,1,![]() ),
),
∴![]() =(0,0,2
=(0,0,2![]() ),
),![]() =(-2,1,
=(-2,1,![]() ),
),
∴cos<![]() ,
,![]() >=
>= =
=![]() ,
,
∴异面直线AO与CD所成角的大小为arccos![]() .
.


练习册系列答案
相关题目
 如图,在Rt△AOB中,
如图,在Rt△AOB中, 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB= 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=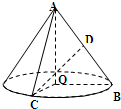 如图,在 Rt△AOB中,
如图,在 Rt△AOB中,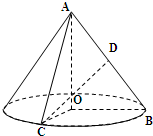 (2009•普陀区一模)如图,在 Rt△AOB中,
(2009•普陀区一模)如图,在 Rt△AOB中,