题目内容
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当D为AB的中点时,求异面直线AO与CD所成角的余弦值大小;
(Ⅲ)求CD与平面AOB所成角最大时的正切值大小.
分析:(1)欲证平面COD⊥平面AOB,先证直线与平面垂直,由题意可得:CO⊥AO,BO⊥AO,CO⊥BO,所以CO⊥平面AOB,进一步易得平面COD⊥平面AOB
(2)解法一:求异面直线所成的角,需要将两条异面直线平移交于一点,由D为AB的中点,故平移时很容易应联想到中位线,作DE⊥OB,垂足为E,连接CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角
解法二:以O为坐标原点,分别以OC、OB、OA为x、y、z轴,建立空间直角坐标系O-xyz.这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(3)本题的设问是递进式的,第(1)问是为第(3)问作铺垫的.求直线与平面所成的角,首先要作出这个平面的垂线,由第(1)问可知:CO⊥平面AOB,所以∠CDO是CD与平面AOB所成的角,tan∠CDO=
=
,当OD最小时,tan∠CDO最大
(2)解法一:求异面直线所成的角,需要将两条异面直线平移交于一点,由D为AB的中点,故平移时很容易应联想到中位线,作DE⊥OB,垂足为E,连接CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角
解法二:以O为坐标原点,分别以OC、OB、OA为x、y、z轴,建立空间直角坐标系O-xyz.这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(3)本题的设问是递进式的,第(1)问是为第(3)问作铺垫的.求直线与平面所成的角,首先要作出这个平面的垂线,由第(1)问可知:CO⊥平面AOB,所以∠CDO是CD与平面AOB所成的角,tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
解答: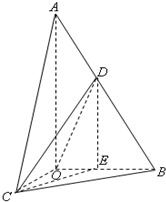 解:(I)由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,
解:(I)由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,
又∵二面角B-AO-C是直二面角,
∴CO⊥BO,
又∵AO∩BO=O,
∴CO⊥平面AOB,
又CO?平面COD,
∴平面COD⊥平面AOB.(4分)
(II)解法一:作DE⊥OB,垂足为E,连接CE(如图),则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.
在 Rt△COE中,CO=BO=2,OE=
BO=1,
∴CE=
=
.
又DE=
AO=
.
∴CD=
=2
∴在Rt△CDE中,cos∠CDE=
=
=
.
∴异面直线AO与CD所成角的余弦值大小为
.(9分)
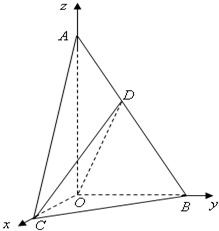 解法二:建立空间直角坐标系O-xyz,如图,
解法二:建立空间直角坐标系O-xyz,如图,
则O(0,0,0),A(0,0,2
),C(2,0,0),D(0,1,
),
∴
=(0,0,2
),
=(-2,1,
),
∴cos<
,
>=
=
=
.
∴异面直线AO与CD所成角的余弦值为
.(9分)
(III)由(I)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角,
且tanCDO=
=
.当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,OD=
=
,tanCDO=
,
∴CD与平面AOB所成角的最大时的正切值为
.(14分)
 解:(I)由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,
解:(I)由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,又∵二面角B-AO-C是直二面角,
∴CO⊥BO,
又∵AO∩BO=O,
∴CO⊥平面AOB,
又CO?平面COD,
∴平面COD⊥平面AOB.(4分)
(II)解法一:作DE⊥OB,垂足为E,连接CE(如图),则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.
在 Rt△COE中,CO=BO=2,OE=
| 1 |
| 2 |
∴CE=
| CO2+OE2 |
| 5 |
又DE=
| 1 |
| 2 |
| 3 |
∴CD=
| CE2+DE2 |
| 2 |
∴在Rt△CDE中,cos∠CDE=
| DE |
| CD |
| ||
2
|
| ||
| 4 |
∴异面直线AO与CD所成角的余弦值大小为
| ||
| 4 |
 解法二:建立空间直角坐标系O-xyz,如图,
解法二:建立空间直角坐标系O-xyz,如图,则O(0,0,0),A(0,0,2
| 3 |
| 3 |
∴
| OA |
| 3 |
| CD |
| 3 |
∴cos<
| OA |
| CD |
| ||||
|
|
| 6 | ||||
2
|
| ||
| 4 |
∴异面直线AO与CD所成角的余弦值为
| ||
| 4 |
(III)由(I)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角,
且tanCDO=
| OC |
| OD |
| 2 |
| OD |
| OA•OB |
| AB |
| 3 |
2
| ||
| 3 |
∴CD与平面AOB所成角的最大时的正切值为
2
| ||
| 3 |
点评:本小题主要考查空间线面关系、异面直线所成的角的度量、线面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB= 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB= 如图,在 Rt△AOB中,
如图,在 Rt△AOB中, (2009•普陀区一模)如图,在 Rt△AOB中,
(2009•普陀区一模)如图,在 Rt△AOB中,