Question

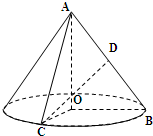（2009•普陀区一模）如图，在 Rt△AOB中，∠OAB=

π

6

，斜边AB=4，D是AB的中点．现将 Rt△AOB以直角边AO为轴旋转一周得到一个圆锥体，点C为圆锥体底面圆周上的一点，且∠BOC=90°．
（1）求该圆锥体的体积；
（2）求异面直线AO与CD所成角的大小．

Answer 1

分析：（1）在 Rt△AOB中，∠OAB=

π

6

，斜边AB=4，所以OC=2，AO=2

3

，该圆锥体的体积v=

1

3

×π×22×2

3

=

8 3

3

π．
（2）解法一、设OB中点为E，连接CE、DE，则设异面直线AO与CD所成角即为∠CDE．由DE∥AO，所以DE⊥底面COB，于是DE⊥CE．又DE=

1

2

AO=

3

，CE=

CO2+EO2

=

5

．由此能求出异面直线AO与CD所成角的大小．
解法二：以OC为x轴，OB为y轴，OA为z轴，建立空间直角坐标系，则

OA

=(0，0，2

3

)，

CD

=(-2，1，

3

)，设异面直线AO与CD所成角为θ，则cosθ=

| OA • CD |

| OA |•| CD |

=

6

2 3 •2 2

=

6

4

．由此能求出异面直线AO与CD所成角的大小．

解答：解：（1）∵在 Rt△AOB中，∠OAB=

π

6

，斜边AB=4，
∴OC=2，AO=2

3

，
该圆锥体的体积v=

1

3

×π×22×2

3

=

8 3

3

π．
（2）解法一、设OB中点为E，连接CE、DE，
则设异面直线AO与CD所成角即为∠CDE．
由DE∥AO，所以DE⊥底面COB，
于是DE⊥CE．
又DE=

1

2

AO=

3

，
CE=

CO2+EO2

=

5

，
∴tan∠CDE=

15

3

．
即异面直线AO与CD所成角的大小为arctan

15

3

．
解法二：以OC为x轴，OB为y轴，OA为z轴，建立空间直角坐标系，
则O（0，0，0），A(0，0，2

3

)，C（2，0，0），D(0，1，

3

)，
∴

OA

=(0，0，2

3

)，

CD

=(-2，1，

3

)，
设异面直线AO与CD所成角为θ，
则cosθ=

| OA • CD |

| OA |•| CD |

=

6

2 3 •2 2

=

6

4

．
∴异面直线AO与CD所成角的大小为arccos

6

4

．

点评：本题考查圆锥体的体积和两条异面直线所成角的大小的求法，解题时要认真审题，合理地建立空间直角坐标系，利用向量法求解两条异面直线所成角的大小．