题目内容
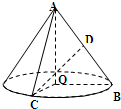 如图,在 Rt△AOB中,∠OAB=
如图,在 Rt△AOB中,∠OAB=| π | 6 |
(1)求异面直线AO与CD所成角的大小;
(2)若某动点在圆锥体侧面上运动,试求该动点从点C出发运动到点D所经过的最短距离.
分析:(1)解法一:设OB中点为E,连接CE、DE,则设异面直线AO与CD所成角即为∠CDE,然后在直角三角形CDE中求出此角即可.
解法二:以OC为x轴,OB为y轴,OA为z轴,建立空间直角坐标系,然后求出异面直线AO与CD的方向向量,最后根据向量的夹角公式cosθ=
进行计算即可求出所求;
(2)由条件,底面圆周长为2π•OB=4π,母线长AB=4,从而求出该圆锥体侧面展开图的扇形圆心角大小,展开图恰好为一个半圆,此时CD的长即为所求,利用余弦定理解之即可.
解法二:以OC为x轴,OB为y轴,OA为z轴,建立空间直角坐标系,然后求出异面直线AO与CD的方向向量,最后根据向量的夹角公式cosθ=
|
| ||||
|
|
(2)由条件,底面圆周长为2π•OB=4π,母线长AB=4,从而求出该圆锥体侧面展开图的扇形圆心角大小,展开图恰好为一个半圆,此时CD的长即为所求,利用余弦定理解之即可.
解答:解:(1)解法一:设OB中点为E,连接CE、DE,则设异面直线AO与CD所成角即为∠CDE.
由DE∥AO,所以DE⊥底面COB,于是DE⊥CE.
又DE=
AO=
,CE=
=
,∴tan∠CDE=
.
即异面直线AO与CD所成角的大小为arctan
.
解法二:以OC为x轴,OB为y轴,OA为z轴,建立空间直角坐标系,则O(0,0,0),A(0,0,2
),C(2,0,0),D(0,1,
),∴
=(0,0,2
),
=(-2,1,
),设异面直线AO与CD所成角为θ,则cosθ=
=
=
.∴异面直线AO与CD所成角的大小为arccos
.
(2)由条件,底面圆周长为2π•OB=4π,母线长AB=4.故该圆锥体侧面展开图的扇形圆心角大小为θ=
=
=π,即展开图恰好为一个半圆.由条件∠BOC=
,故展开图中,∠CAB=
,此时CD的长即为所求.由余弦定理,CD2=CA2+AD2-2CA•AD•cos45°=20-8
,故从点C出发在圆锥体表面运动到点D的最短距离为2
.
由DE∥AO,所以DE⊥底面COB,于是DE⊥CE.
又DE=
| 1 |
| 2 |
| 3 |
| CO2+EO2 |
| 5 |
| ||
| 3 |
即异面直线AO与CD所成角的大小为arctan
| ||
| 3 |
解法二:以OC为x轴,OB为y轴,OA为z轴,建立空间直角坐标系,则O(0,0,0),A(0,0,2
| 3 |
| 3 |
| OA |
| 3 |
| CD |
| 3 |
|
| ||||
|
|
| 6 | ||||
2
|
| ||
| 4 |
| ||
| 4 |
(2)由条件,底面圆周长为2π•OB=4π,母线长AB=4.故该圆锥体侧面展开图的扇形圆心角大小为θ=
| 2πr |
| l |
| 4π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 2 |
5-2
|
点评:本题主要考查了两异面直线所成角,以及旋转体表面上的最短距离问题,属于中档题.

练习册系列答案
相关题目
 如图,在Rt△AOB中,
如图,在Rt△AOB中, 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB= 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=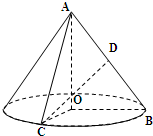 (2009•普陀区一模)如图,在 Rt△AOB中,
(2009•普陀区一模)如图,在 Rt△AOB中,