题目内容
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
(1)求证:平面COD⊥平面AOB;
(2)设CD与平面AOB所成角的最大值为α,求tanα值.
分析:(1)利用二面角的定义、线面与面面垂直的判定与性质即可得出;
(2)利用线面角的定义及其含30°角的直角三角形的边角关系即可得出.
(2)利用线面角的定义及其含30°角的直角三角形的边角关系即可得出.
解答:证明:(1)由已知CO⊥AO,BO⊥AO,
∴∠BOC是二面角B-AO-C的平面角,
∴∠BOC=
,∴OC⊥OB.
∵OA∩OB=O,∴OC⊥平面AOB,
∴平面COD⊥平面AOB;
(2)由(1)可知CO⊥平面OAB,∴∠CDO是CD与平面AOB所成的角.
∴tan∠CDO=
,
∵OC=OB=2,
∴当OD⊥AB时,OD取得最小值=OB•sin60°=
,此时∠CDO取得最大值α,
且tanα=
=
.
∴∠BOC是二面角B-AO-C的平面角,
∴∠BOC=
| π |
| 2 |
∵OA∩OB=O,∴OC⊥平面AOB,
∴平面COD⊥平面AOB;
(2)由(1)可知CO⊥平面OAB,∴∠CDO是CD与平面AOB所成的角.
∴tan∠CDO=
| CO |
| OD |
∵OC=OB=2,
∴当OD⊥AB时,OD取得最小值=OB•sin60°=
| 3 |
且tanα=
| 2 | ||
|
2
| ||
| 3 |
点评:熟练掌握二面角的定义、线面与面面垂直的判定与性质、线面角的定义及其含30°角的直角三角形的边角关系是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△AOB中,
如图,在Rt△AOB中, 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=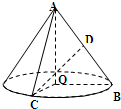 如图,在 Rt△AOB中,
如图,在 Rt△AOB中,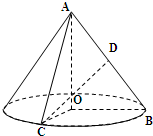 (2009•普陀区一模)如图,在 Rt△AOB中,
(2009•普陀区一模)如图,在 Rt△AOB中,