题目内容
设数列{an}是公差为d的等差数列,其前n项和为Sn.
(1)已知a1=1,d=2,
(i)求当n∈N*时,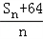 的最小值;
的最小值;
(ii)当n∈N*时,求证: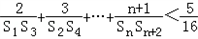 ;
;
(2)是否存在实数a1,使得对任意正整数n,关于m的不等式am≥n的最小正整数解为3n﹣2?若存在,则求a1的取值范围;若不存在,则说明理由.
(1)已知a1=1,d=2,
(i)求当n∈N*时,
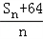 的最小值;
的最小值;(ii)当n∈N*时,求证:
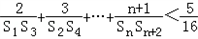 ;
;(2)是否存在实数a1,使得对任意正整数n,关于m的不等式am≥n的最小正整数解为3n﹣2?若存在,则求a1的取值范围;若不存在,则说明理由.
解:(1)(i)解:∵a1=1,d=2,
∴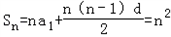 ,
,
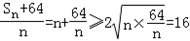 ,
,
当且仅当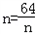 ,即n=8时,上式取等号.
,即n=8时,上式取等号.
故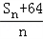 的最小值是16.
的最小值是16.
(ii)证明:由(i)知Sn=n2,
当n∈N*时,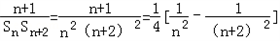 ,
,
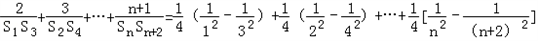
=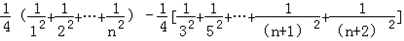
=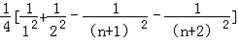 ,
,
∵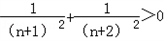 ,
,
∴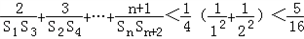 .
.
(2)假设对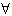 n∈N*,关于m的不等式
n∈N*,关于m的不等式
am=a1+(m﹣1)d≥n的最小正整数解为cn=3n﹣2,
当n=1时,a1+(c1﹣1)d=a1≥1;
当n≥2时,恒有
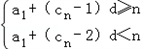 ,
,
即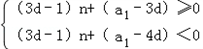 ,
,
从而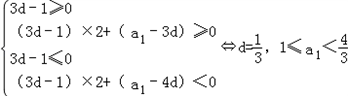 .
.
当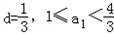 时,对
时,对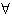 n∈N*,且n≥2时,
n∈N*,且n≥2时,
当正整数m<cn时,有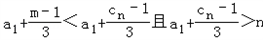 .
.
a1符合题意且a1的取值范围是 .
.
∴
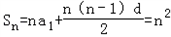 ,
,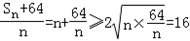 ,
,当且仅当
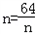 ,即n=8时,上式取等号.
,即n=8时,上式取等号.故
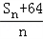 的最小值是16.
的最小值是16.(ii)证明:由(i)知Sn=n2,
当n∈N*时,
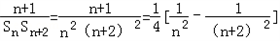 ,
,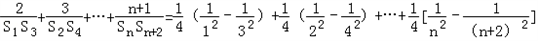
=
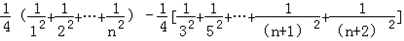
=
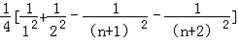 ,
,∵
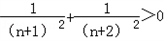 ,
,∴
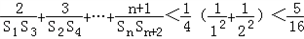 .
.(2)假设对
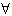 n∈N*,关于m的不等式
n∈N*,关于m的不等式am=a1+(m﹣1)d≥n的最小正整数解为cn=3n﹣2,
当n=1时,a1+(c1﹣1)d=a1≥1;
当n≥2时,恒有
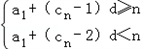 ,
,即
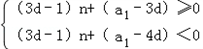 ,
,从而
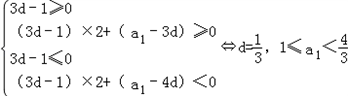 .
.当
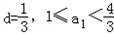 时,对
时,对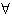 n∈N*,且n≥2时,
n∈N*,且n≥2时,当正整数m<cn时,有
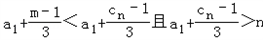 .
.a1符合题意且a1的取值范围是
 .
.
练习册系列答案
相关题目