题目内容
(2013•南京二模)设数列{an}是公差不为0的等差数列,Sn为其前n项和,若
+
=
+
,S5=5,则a7的值为
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| a | 2 4 |
9
9
.分析:设出等差数列的公差,由题意列关于首项和公差的二元一次方程组,求出首项和公差,则a7的值可求.
解答:解:设等差数列{an}的公差为d(d≠0),由
+
=
+
,S5=5,
得
,
整理得
,解得
.
所以a7=a1+6d=-3+6×2=9.
故答案为9.
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| a | 2 4 |
得
|
整理得
|
|
所以a7=a1+6d=-3+6×2=9.
故答案为9.
点评:本题考查了等差数列的通项公式和前n项和公式,考查了学生的计算能力,是基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
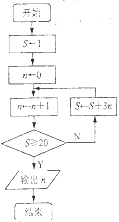 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是