题目内容
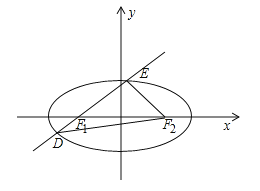
【题目】已知点![]() ,点
,点![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,直线
的左右顶点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点.当
为坐标原点.当![]() 为直角时,求直线
为直角时,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意知,求得![]() ,再由
,再由![]() ,代入椭圆方程,解得
,代入椭圆方程,解得![]() ,即可得到椭圆的方程;
,即可得到椭圆的方程;
(2)设l的方程为y=kx+2,与椭圆的方程联立方程组,利用二次方程中根与系数的关系,求得![]() ,又由∠MON能为直角时,利用
,又由∠MON能为直角时,利用![]() 列出方程,即可求解.
列出方程,即可求解.
(1)由题意知,a=2,B(2,0),设Q(x0,y0),由![]() ,得
,得![]() ,
,
代入椭圆方程,解得b2=1. ∴椭圆方程为![]() .
.
(2)由题意可知,直线l的斜率存在,令l的方程为y=kx+2,M(x1,y1),N(x2,y2),
则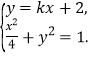 整理得:(1+4k2)x2+16kx+12=0,
整理得:(1+4k2)x2+16kx+12=0,
由直线l与E有两个不同的交点,则△>0,
即(16k)2﹣4×12×(1+4k2)>0,解得![]() .
.
由韦达定理可知:![]() .
.
当∠MON能为直角时,![]() ,即
,即![]() ,
,
则x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
![]() ,解得k2=4,即
,解得k2=4,即![]() .
.
综上可知,直线l的斜率![]() 时,∠MON为直角.
时,∠MON为直角.

练习册系列答案
相关题目