题目内容
15．已知$\overrightarrow{a}$⊥$\overrightarrow{b}$，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，且$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-λ$\overrightarrow{b}$垂直，则实数λ=4．分析 由已知条件，$\overrightarrow{a}•\overrightarrow{b}=0$，$（\overrightarrow{a}+\overrightarrow{b}）•（\overrightarrow{a}-λ\overrightarrow{b}）=0$，所以可得到${\overrightarrow{a}}^{2}-λ{\overrightarrow{b}}^{2}=4-λ$=0，这就求出了λ．
解答 解：根据已知条件：$\overrightarrow{a}•\overrightarrow{b}=0$；
∴$（\overrightarrow{a}+\overrightarrow{b}）•（\overrightarrow{a}-λ\overrightarrow{b}）={\overrightarrow{a}}^{2}-λ{\overrightarrow{b}}^{2}$=4-λ=0；
∴λ=4．
故答案为：4．
点评 考查两非零向量垂直的充要条件，向量数量积的运算．
练习册系列答案
相关题目
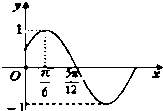已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图，令${a_n}=f（\frac{nπ}{6}）$，则a1+a2+a3+…+a2014=0．