题目内容
【题目】在平面直角坐标系中，设
的顶点分别为
，圆
是的外接圆，直线
的方程是
.
（1）求圆的方程；
（2）证明：直线与圆相交；
（3）若直线被圆截得的弦长为3，求的方程．
【答案】（1）
；（2）证明见解析；（3）
或
.
【解析】
（1）求出边AC、BC的垂直平分线方程，根据圆心M在这2条边的垂直平分线上，可得M（
,），再求出半径MC的值，即可得到圆的标准方程．（2）根据直线l经过定点N，而点N在圆的内部，即可得到直线和圆相交．（3）由条件利用弦长公式求得圆心M（,）到直线l的距离为d=．再根据据点到直线的距离公式求得m的值，可得直线l的方程．
（1）∵△ABC的顶点分别为A（0，2），B（﹣1，0），C（2，0），故线段BC的垂直平分线方程为x＝
，
线段AC的垂直平分线为 y＝x，再由圆心M在这2条边的垂直平分线上，可得M（，），
故圆的半径为|MC|＝
＝
，故圆的方程为
+
＝
．
（2）根据直线l的方程是（2+m）x+（2m﹣1）y﹣3m﹣1＝0（m∈R），即m（x+2y﹣3）+2x﹣y﹣1＝0，
由
可得
，故直线经过定点N（1，1）．
由于MN＝
＝
＜r＝
，故点N在圆的内部，故圆和直线相交．
（3）∵直线l被圆M截得的弦长为3，
故圆心M（
，）到直线l的距离为d＝
＝．
再根据点到直线的距离公式可得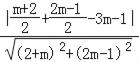
＝
，求得 m＝﹣2，或m＝，
故直线l的方程为y＝1或x＝1．
小学课时特训系列答案
【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表：
原料 | 磷酸盐（单位：吨） | 硝酸盐（单位：吨） |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨，计划在此基础上生产若干车皮的甲、乙两种混合肥料．
（1）设x，y分别表示计划生产甲、乙两种肥料的车皮数，试列出x，y满足的数学关系式，并画出相应的平面区域；
（2）若生产1车皮甲种肥料，利润为3万元；生产1车皮乙种肥料，利润为2万元．那么分别生产甲、乙两种肥料多少车皮，能够产生最大利润？最大利润是多少？
