题目内容
【题目】.(本小题满分14分)已知等比数列![]() 的公比为
的公比为![]() ,首项为
,首项为![]() ,其前
,其前![]() 项的和为
项的和为![]() .数列
.数列![]() 的前
的前![]() 项的和为
项的和为![]() , 数列
, 数列![]() 的前
的前![]() 项的和为
项的和为![]()
(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当![]() 为奇数时,比较
为奇数时,比较![]() 与
与![]() 的大小; ②当
的大小; ②当![]() 为偶数时,若
为偶数时,若![]() ,问是否存在常数
,问是否存在常数![]() (与n无关),使得等式
(与n无关),使得等式![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
【答案】解: (Ⅰ)∵![]()
![]() , ∴
, ∴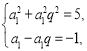 ∴
∴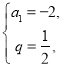 或
或![]() ………………2分
………………2分
∴![]() ,或
,或![]() . ……………………………………4分
. ……………………………………4分
(Ⅱ) ∵![]() 常数,
常数, ![]() =常数,
=常数,
∴数列![]() ,
,![]() 均为等比数列,首项分别为
均为等比数列,首项分别为![]() ,
,![]() ,公比分别为
,公比分别为![]() ,
,![]() .………………6分
.………………6分
①当![]() 为奇数时, 当
为奇数时, 当![]() 时,
时, ![]() ,
,![]() ,
,![]() , ∴
, ∴![]() .
.
当![]() 时,
时, ![]() ,
,![]() ,
,![]() , ∴
, ∴![]() . ……………………8分
. ……………………8分
当![]() 时, 设
时, 设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴![]() . 综上所述,当
. 综上所述,当![]() 为奇数时,
为奇数时,![]() . ……………………10分
. ……………………10分
②当![]() 为偶数时,∵
为偶数时,∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
∴![]() =
=![]()
![]()
![]() =
=![]() ………………………………12分
………………………………12分
由题设,![]() 对所有的偶数n恒成立,又
对所有的偶数n恒成立,又![]() ,∴
,∴![]() .………………13分
.………………13分
∴存在常数![]() ,使得等式
,使得等式![]() 恒成立.………………………………14分
恒成立.………………………………14分
【解析】略

练习册系列答案
相关题目
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元