题目内容
5.已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ACB=$\frac{π}{3}$,点D是线段BC的中点.(1)求证:A1C∥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
分析 (1)设A1B∩AB1=O,连接OD,利用三角形的中位线定理可得:A1C∥OD,利用线面平行的判定定理即可证明;
(2)当三棱柱ABC-A1B1C1的底面积最大时,体积最大,利用余弦定理与基本不等式的性质可得:当AC=BC,三角形ABC为正三角形时取最大值,然后建立空间直角坐标系,利用空间向量求直线A1D与平面AB1D所成角θ的正弦值.
解答 (1)证明:如图,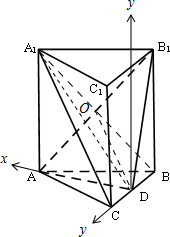 设A1B∩AB1=O,连接OD,
设A1B∩AB1=O,连接OD,
则OD为三角形A1BC的中位线,
∴A1C∥OD,OD⊆平面AB1D,A1C?平面AB1D,
∴A1C∥平面AB1D;
(2)解:当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵$4=A{B}^{2}=A{C}^{2}+B{C}^{2}-2AC•BC•cos\frac{π}{3}≥$2AC•BC-AC•BC=AC•BC,
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
以D为原点建立如图所示坐标系,
则D(0,0,0),A($\sqrt{3}$,0,0),B1(0,-1,2),${A}_{1}(\sqrt{3},0,2)$,
∴$\overrightarrow{DA}$=($\sqrt{3}$,0,0),$\overline{D{B}_{1}}$=(0,-1,2),$\overline{D{A}_{1}}=(\sqrt{3},0,2)$,
设平面AB1D的法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DA}=0}\\{\overrightarrow{n}•\overrightarrow{D{B}_{1}}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\sqrt{3}x=0}\\{-y+2z=0}\end{array}\right.$,取z=1,得y=2.
∴$\overrightarrow{n}=(0,2,1)$,
则直线A1D与平面AB1D所成角θ的正弦值为sinθ=|$\frac{\overrightarrow{n}•\overrightarrow{D{A}_{1}}}{|\overrightarrow{n}|•|\overrightarrow{D{A}_{1}}|}$|=|$\frac{2}{\sqrt{5}×\sqrt{7}}$|=$\frac{2\sqrt{35}}{35}$.
点评 本题考查了线面面面垂直与平行的判定与性质定理、三角形的中位线定理、余弦定理,考查了推理能力与计算能力,考查了空间想象能力,训练了利用空间向量求线面角,属于中档题.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | 6+2sin2 | B. | -6-2cos2 | C. | 20 | D. | -20 |
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |