Question

9．已知三角形两边长分别为4和2$\sqrt{3}$，第三条边上的中线长为$\sqrt{5}$，则三角形的外接圆半径为$\frac{6\sqrt{33}}{11}$．

Answer 1

分析 设AB=4，AC=2$\sqrt{3}$，AD=$\sqrt{5}$，D为BC边的中点，BC=2x，则BD=DC=x，利用余弦定理以及cos∠ADB=-cos∠ADC，求得x的值，可得BC的值．利用余弦定理求得cosA的值，可得sinA的值，再利用正弦定理求得外接圆的直径2R，可得三角形的外接圆半径．

解答 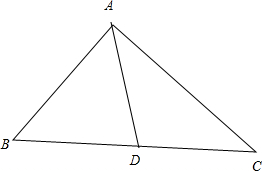解：设AB=4，AC=2$\sqrt{3}$，AD=$\sqrt{5}$，D为BC边的中点，BC=2x，则BD=DC=x．
△ABD中，由余弦定理可得cos∠ADB=$\frac{{x}^{2}+5-16}{2x\sqrt{5}}$，
△ADC中，由余弦定理可得，cos∠ADC=$\frac{{x}^{2}+5-12}{2x\sqrt{5}}$．
再根据cos∠ADB=-cos∠ADC，可得 $\frac{{x}^{2}+5-16}{2x\sqrt{5}}$=-$\frac{{x}^{2}+5-12}{2x\sqrt{5}}$，∴x=3，
∴BC=6．
再根据余弦定理可得AB²+AC²-BC² =2AB•AC•cosA，即 16+12-36=2×4×2$\sqrt{3}$×cosA，
求得cosA=-$\frac{\sqrt{3}}{6}$，∴sinA=$\frac{\sqrt{33}}{6}$，
∴外接圆的直径2R=$\frac{BC}{sinA}$=$\frac{6}{\frac{\sqrt{33}}{6}}$=$\frac{12\sqrt{33}}{11}$，从而可得R=$\frac{6\sqrt{33}}{11}$
故答案为：$\frac{6\sqrt{33}}{11}$．

点评 本题主要考查了利用余弦定理求解三角形的应用，直角三角形的性质的应用，属于三角知识的综合应用，属于中档题．