题目内容
【题目】设![]()
(1)证明:当![]() 时,
时,![]() ;
;
(2)当![]() 时
时![]() ,求整数
,求整数![]() 的最大值.(参考数据:
的最大值.(参考数据:![]() ,
,![]() )
)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)将![]() 代入函数解析式可得
代入函数解析式可得![]() ,构造函数
,构造函数![]() ,求得
,求得![]() 并令
并令![]() ,由导函数符号判断函数单调性并求得最大值,由
,由导函数符号判断函数单调性并求得最大值,由![]() 即可证明
即可证明![]() 恒成立,即不等式得证.
恒成立,即不等式得证.
(2)对函数求导,变形后讨论当![]() 时的函数单调情况:当
时的函数单调情况:当![]() 时,可知满足题意;将不等式化简后构造函数
时,可知满足题意;将不等式化简后构造函数![]() ,利用导函数求得极值点与函数的单调性,从而求得最小值为
,利用导函数求得极值点与函数的单调性,从而求得最小值为![]() ,分别依次代入检验
,分别依次代入检验![]() 的符号,即可确定整数
的符号,即可确定整数![]() 的最大值;当
的最大值;当![]() 时不满足题意,因为求整数
时不满足题意,因为求整数![]() 的最大值,所以
的最大值,所以![]() 时无需再讨论.
时无需再讨论.
(1)证明:当![]() 时代入
时代入![]() 可得
可得![]() ,
,
令![]() ,
,![]() ,
,
则![]() ,
,
令![]() 解得
解得![]() ,
,
当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,
则![]() ,即
,即![]() 成立.
成立.
(2)函数![]()
则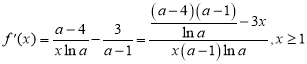 ,
,
若![]() 时,当
时,当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,即当
,即当![]() 时
时![]() 成立;
成立;
所以此时需满足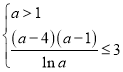 的整数解即可,
的整数解即可,
将不等式化简可得![]() ,
,
令![]()
则![]()
令![]() 解得
解得![]() ,
,
当![]() 时
时![]() ,即
,即![]() 在
在![]() 内单调递减,
内单调递减,
当![]() 时
时![]() ,即
,即![]() 在
在![]() 内单调递增,
内单调递增,
所以当![]() 时
时![]() 取得最小值,
取得最小值,
则![]() ,
,
![]() ,
,
![]() ,
,
![]()
所以此时满足![]() 的整数
的整数![]() 的最大值为
的最大值为![]() ;
;
当![]() 时,在
时,在![]() 时
时![]() ,此时
,此时![]() ,与题意矛盾,所以不成立.
,与题意矛盾,所以不成立.
因为求整数![]() 的最大值,所以
的最大值,所以![]() 时无需再讨论,
时无需再讨论,
综上所述,当![]() 时
时![]() ,整数
,整数![]() 的最大值为
的最大值为![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中![]() 表示通过自主招生获得降分资格的学生人数,
表示通过自主招生获得降分资格的学生人数,![]() 表示被清华、北大等名校录取的学生人数)
表示被清华、北大等名校录取的学生人数)
年份(届) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通过画散点图发现![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(保留两位有效数字)
的线性回归方程;(保留两位有效数字)
(2)若已知该校2019年通过自主招生获得降分资格的学生人数为61人,预测2019年高考该校考人名校的人数;
(3)若从2014年和2018年考人名校的学生中采用分层抽样的方式抽取出5个人回校宣传,在选取的5个人中再选取2人进行演讲,求进行演讲的两人是2018年毕业的人数![]() 的分布列和期望.
的分布列和期望.
参考公式: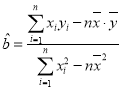 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()