题目内容
已知函数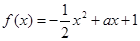 ,
,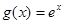 ,
,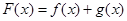 .
.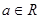
(1)若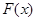 在
在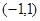 存在极值,求
存在极值,求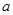 的取值范围;
的取值范围;
(2)若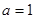 ,问是否存在与曲线
,问是否存在与曲线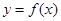 和
和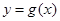 都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
(1)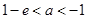 (2)存在一条公切线,切线方程为:
(2)存在一条公切线,切线方程为: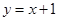
解析试题分析:(Ⅰ) 依题有: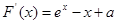 则
则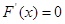 在
在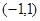 上有变号零点;
上有变号零点;
令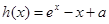 ,则
,则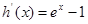
当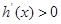 ,则
,则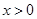 ;当
;当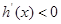 ,则
,则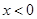
因此,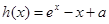 在
在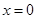 处取得极小值。 3分
处取得极小值。 3分
而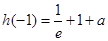 ,
,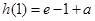 ,
,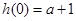
易知,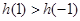
①当存在两个变号零点时,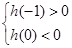 ,可得:
,可得: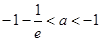
② 当存在一个变号零点时,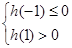 ,可得:
,可得: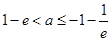
综上,当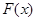 在
在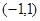 上存在极值时,
上存在极值时,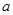 的范围为:
的范围为: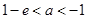 6分
6分
(Ⅱ) 当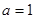 时,
时, ,
,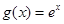
易知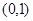 是
是 与
与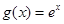 的一个公共点。
的一个公共点。
若有公共切线,则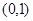 必为切点,∵
必为切点,∵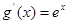 ,∴
,∴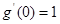
可知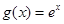 在
在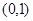 处的切线为
处的切线为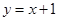
而 ,∴
,∴ 则
则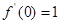
可知 在
在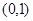 处的切线也为
处的切线也为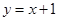
因此,存在一条公切线,切线方程为: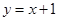 。 12分
。 12分
考点:函数单调性极值最值
点评:函数在某区间有极值,则在区间上有变号零点,转化为导函数最大值最小值一正一负,第二问找到两函数的公共点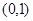 是求解的关键,只需求在该点处的两条切线看其是否相同
是求解的关键,只需求在该点处的两条切线看其是否相同

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 在
在 处取得极值.
处取得极值. 的值;
的值;  的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; ,不等式
,不等式 都成立.
都成立. 和“伪二次函数”
和“伪二次函数” 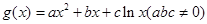 .
. ,无论
,无论 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数; ),B(
),B( ),线段AB中点为C(
),线段AB中点为C( ),记直线AB的斜率为k.
),记直线AB的斜率为k. ;
; ,是否有(1)同样的性质?证明你的结论。
,是否有(1)同样的性质?证明你的结论。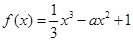
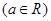 .
. (
( 且
且 ).
). 时,求证:
时,求证: 在
在 上单调递增;
上单调递增; 且
且 时,求证:
时,求证: .
.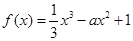
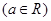 .
.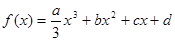 (
( >0),且方程
>0),且方程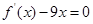 的两个根分别为1,4。
的两个根分别为1,4。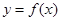 过原点时,求
过原点时,求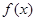 的解析式;
的解析式;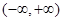 无极值点,求a的取值范围。
无极值点,求a的取值范围。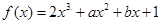 的导数为
的导数为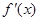 ,若函数
,若函数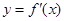 的图像关于直
的图像关于直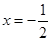 对称,且
对称,且 . (1)求实数
. (1)求实数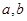 的值 ;(2)求函数
的值 ;(2)求函数 的极值.
的极值.