题目内容
3.已知sinα-3cosα=0,则sin2α+sinαcosα-2=-$\frac{4}{5}$.分析 由已知可得tanα=3,将sin2α+sinαcosα-2利用弦化切思想,化为$\frac{{tan}^{2}α+tanα}{{tan}^{2}α+1}$-2可得答案.
解答 解:∵sinα-3cosα=0,
∴sinα=3cosα,即tanα=3,
∴sin2α+sinαcosα-2=$\frac{{sin}^{2}α+sinαcosα}{{sin}^{2}α+{cos}^{2}α}$-2=$\frac{{tan}^{2}α+tanα}{{tan}^{2}α+1}$-2=$\frac{12}{10}$-2=-$\frac{4}{5}$,
故答案为:-$\frac{4}{5}$.
点评 本题考查的知识点是同角三角函数基本关系的运算,弦化切思想,难度中档.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
8.设向量$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(1,x),记f(x)为向量$\overrightarrow{b}$在$\overrightarrow{a}$上投影的数量,已知x∈(-π,π),则f(x)为( )
| A. | 既是奇函数又是偶函数 | B. | 偶函数,且有两个零点 | ||
| C. | 奇函数,且有三个零点 | D. | 偶函数,且只有一个极值点 |
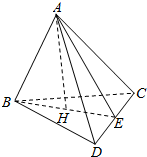 如图所示,已知空间四边形ABCD的边BC=AC,AD=BD,BE⊥CD于点E,AH⊥BE于点H,求证:AH⊥平面BCD.
如图所示,已知空间四边形ABCD的边BC=AC,AD=BD,BE⊥CD于点E,AH⊥BE于点H,求证:AH⊥平面BCD.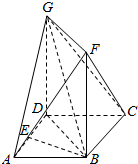 如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.
如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.