题目内容
18.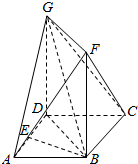 如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.
如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.(1)求证:BE⊥平面BCF;
(2)求直线AF与平面BCG所成角的正弦值.
分析 (1)由已知推导出BE⊥BC,BF⊥BC,由此能证明BE⊥平面BCF.
(2)以B为原点,EB延长线为x轴,BC为y轴,BF为z轴,建立空间直角坐标系,利用向量法能求出直线AF与平面BCG所成角的正弦值.
解答  证明:(1)∵在菱形ABCD中,∠DAB=60°,E为AD的中点,
证明:(1)∵在菱形ABCD中,∠DAB=60°,E为AD的中点,
∴BE⊥AD,∵AD∥BC,∴BE⊥BC,
∵正方形DBFG所在平面与平面ABCD垂直,
∴BF⊥BD,∴BF⊥平面ABCD,∴BF⊥BC,
∵BF∩BC=B,
∴BE⊥平面BCF.
解:(2)以B为原点,EB延长线为x轴,BC为y轴,BF为z轴,建立空间直角坐标系,
设AB=2,则A(-$\sqrt{3}$,-1,0),F(0,0,2),
B(0,0,0),C(0,2,0),G(-$\sqrt{3}$,1,2),
$\overrightarrow{AF}$=($\sqrt{3}$,1,2),$\overrightarrow{BG}$=(-$\sqrt{3}$,1,2),$\overrightarrow{BC}$=(0,2,0),
设平面BCG的法向量$\overrightarrow{n}$=(x,y,z),111111111111
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BG}=-\sqrt{3}x+y+2z=0}\\{\overrightarrow{n}•\overrightarrow{BC}=2y=0}\end{array}\right.$,
取x=4$\sqrt{3}$,得$\overrightarrow{n}$=(4$\sqrt{3}$,0,6),
设直线AF与平面BCG所成角为θ,
则sinθ=|cos<$\overrightarrow{n},\overrightarrow{AF}$>|=|$\frac{\overrightarrow{n}•AF}{|\overrightarrow{n}|•|\overrightarrow{AF}|}$|=|$\frac{12+12}{2\sqrt{2}•2\sqrt{21}}$|=$\frac{\sqrt{42}}{7}$.
∴直线AF与平面BCG所成角的正弦值为$\frac{\sqrt{42}}{7}$.
点评 本题考查线面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 优等生题库系列答案
优等生题库系列答案| A. | (-∞,-2]∪[3,+∞) | B. | [2,3] | C. | (-∞,0]∪[3,+∞) | D. | [0,3] |