Question

13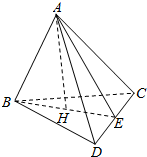．如图所示，已知空间四边形ABCD的边BC=AC，AD=BD，BE⊥CD于点E，AH⊥BE于点H，求证：AH⊥平面BCD．

Answer 1

分析 取AB中点F，连接DF、CF，由已知推导出AB⊥CD，从而得到CD⊥平面ABH，进而CD⊥AH，由此能证明AH⊥平面BCD．

解答 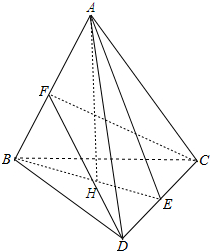证明：取AB中点F，连接DF、CF，
∵AC=BC，AD=BD，
∴DF⊥AB，CF⊥AB，
又∵DF、CF∈平面FCD，DF∩CF=F
∴AB⊥平面FCD，
∵CD?平面FCD，∴AB⊥CD，
又∵BE⊥CD，且BE?平面ABH，BE∩AB=B，
∴CD⊥平面ABH，
∵AH?平面ABH，∴CD⊥AH，
由已知条件，AH⊥BE，BE∩CD=E．
∴AH⊥平面BCD．

点评 本题考查线面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．