题目内容
6.已知命题p:?x∈[0,+∞),($\frac{1}{2}$)x<m;命题q:?x∈R,x2+2>m2.(1)若(¬p)∧q为真命题,求实数m的取值范围;
(2)若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
分析 若命题p为真命题,则m>1;若命题q为真命题,则$-\sqrt{2}<m<\sqrt{2}$.(1)若(¬p)∧q为真命题,则$\left\{\begin{array}{l}{m≤1}\\{-\sqrt{2}<m<\sqrt{2}}\end{array}\right.$,解得即可.
(2)若p∨q为真命题,p∧q为假命题,则p与q必然一真一假,解出即可.
解答 解:命题p:?x∈[0,+∞),($\frac{1}{2}$)x<m,则m>1;
命题q:?x∈R,x2+2>m2,∴m2<2,解得$-\sqrt{2}<m<\sqrt{2}$.
(1)若(¬p)∧q为真命题,∴$\left\{\begin{array}{l}{m≤1}\\{-\sqrt{2}<m<\sqrt{2}}\end{array}\right.$,解得$-\sqrt{2}<m≤1$.
∴实数m的取值范围是$(-\sqrt{2},1]$;
(2)若p∨q为真命题,p∧q为假命题,
则p与q必然一真一假,
若p真q假,则$\left\{\begin{array}{l}{m>1}\\{m≤-\sqrt{2}或m≥\sqrt{2}}\end{array}\right.$,解得$m≥\sqrt{2}$.
若q真p假,则$\left\{\begin{array}{l}{m≤1}\\{-\sqrt{2}<m<\sqrt{2}}\end{array}\right.$,解得$-\sqrt{2}<m≤1$.
综上可得:实数m的取值范围是$(-\sqrt{2},1]$∪$[\sqrt{2},+∞)$.
点评 本题考查了函数的性质、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
11.已知函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)的图象与函数y=logax(a>0,a≠1)的图象有一个交点,则a的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{2}}{2}$,1)∪(1,4] | D. | (1,4] |
18.若f(x)=ax2-$\sqrt{2}$(a>0),且f($\sqrt{2}$)=2,则a等于( )
| A. | 1+$\frac{\sqrt{2}}{2}$ | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 2 |
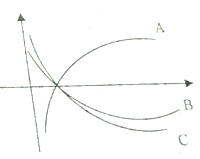 如图:下面三个分别是y=1og2x,y=${log}_{\frac{1}{3}}x$,y=log${\;}_{\frac{1}{4}}$x函数图象,则A代表函数y=1og2x; B代表函数y=log${\;}_{\frac{1}{4}}$x; C代表函数y=1og$\frac{1}{3}$x.
如图:下面三个分别是y=1og2x,y=${log}_{\frac{1}{3}}x$,y=log${\;}_{\frac{1}{4}}$x函数图象,则A代表函数y=1og2x; B代表函数y=log${\;}_{\frac{1}{4}}$x; C代表函数y=1og$\frac{1}{3}$x.