题目内容
(本题满分16分)
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数。
的生成函数。
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由。
的生成函数?并说明理由。
第一组:![]() ;
;
第二组:![]() 。
。
(2)设![]() ,生成函数
,生成函数![]() 。若不等式
。若不等式![]()
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围。
的取值范围。
(3)设![]() ,取
,取![]() 生成函数
生成函数![]() 图象的最低点坐标为
图象的最低点坐标为![]() 。
。
若对于任意正实数![]() 且
且![]() ,
,
试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
(1)①设![]() ,即
,即![]()
取![]() ,所以
,所以![]() 是
是![]() 的生成函数。
的生成函数。
②设![]() ,即
,即![]()
则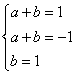 ,该方程组无解。
,该方程组无解。
所以![]() 不是
不是![]() 的生成函数。…………………………………4分
的生成函数。…………………………………4分
(2)![]()
![]() ,即
,即![]()
所以,![]() 。因为
。因为![]() ,所以
,所以![]()
则![]() ,函数
,函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]()
故![]() 。 …………………………………10分
。 …………………………………10分
(3)由题意得,![]() ,则
,则![]() ,故
,故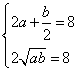 ,解得
,解得![]() 所以
所以![]() 。 …………………………12分
。 …………………………12分
假设存在最大的常数![]() ,使
,使![]() 恒成立。于是设
恒成立。于是设![]()
![]()
=![]()
设![]() ,则
,则![]() ,即
,即![]()
设![]()
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]()
故存在最大的常数![]() …………………………………16分
…………………………………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在